12.1 Introduction
The "airmass" as a general term, describes the ratio of the amount of an attenuating medium integrated along a slanted path through the atmosphere to the amount integrated along a vertical path. It enables the amount of the medium in a vertical column to be derived from measurements of attenuation along the slanted path. In the ozone measurement equations, equation 1.1 and the following equations, three attenuating media are described, ozone, air molecules and aerosol, and each has a slightly different airmass, owing principally to their different height distribution and the sphericity of the atmosphere. However, all are approximately equal to secant Z, where Z is the solar zenith angle at the observing site.
Aerosols are concentrated near the ground and the appropriate airmass is taken to be sec Z, though generally the aerosol term and hence its airmass are neglected. The airmass for scattering by air molecules, m, can be calculated to account for the atmosphere's sphericity and for atmospheric refraction, and has been empirically expressed by Kasten (1966) as:
m = (cos Z + 0.1500 (93.885 - Z)-1.253)-1 (12.1)
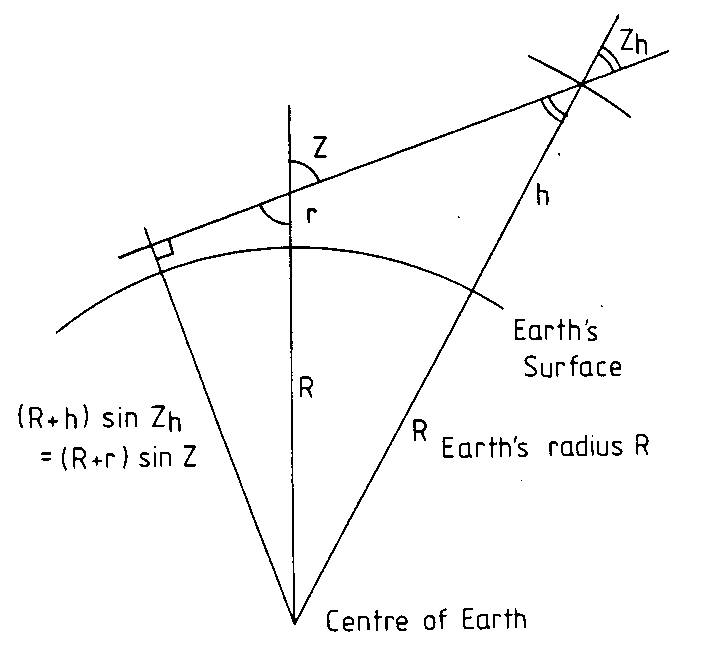
where Z is in degrees. The airmass appropriate to the ozone layer, μh,
is taken as the secant of the zenith angle at the mean height of the
ozone layer, and the mean height has been traditionally assumed to be 22
km (Dobson, 1957a). Figure 12.1 illustrates the geometry of the
situation, and from this it is not difficult to show that:
μh = (cos (arcsin (l sinZ)))-1 (12.2)
or
μh = (1 - l2 sin2 Z)-1/2 (12.3)
where
l = (R + r)/(R + h) ≈ 1 - (h - r)/R (12.4)
As shown in Figure 12.1, h is the mean ozone layer height above mean sea level and r is the altitude of the observing station. Note that h depends on the difference of these, i.e., on h-r, and not on h alone. If h-r = 22 km and R = 6370 km, then l= 0.99655.
Incidentally, the solar zenith angle Z is expressed as:
cos Z = cos φ cos δ cos θ + sin φ sin δ (12.5)
where φ is the station latitude (negative in the Southern Hemisphere), δ is the solar declination (negative from about September 21 to about March 21), and θ is the local hour angle of the sun at the observing station (zero at local apparent noon). Komhyr (1980b) gives a full account of how to determine these parameters, and hence Z and μh, not only for the sun but also for the moon.
12.2 Error analysis
It is useful to compare the three airmass terms: this is done in Table 12.1. The table shows that the differences among the airmass terms are small for small solar zenith angles, but become increasingly important beyond an airmass of 2.
TABLE 12.1 Comparison of sec Z, m and μh, for h-r = 22 km. Z sec Z m μh 10 1.0154 1.0148 1.0153 60 2.0000 1.9928 1.9797 70 2.9238 2.8999 2.8508 75 3.8637 3.8081 3.6911 80 5.7587 5.5803 5.2117 83 8.2054 7.7278 6.8009 85 11.4735 10.3229 8.3292 87 19.1069 15.2186 10.2112
In particular, the use of sec Z in place of μh would contribute errors of 1% at an airmass of 2 and 5% at an airmass of 4. Errors in airmass μh transfer to ozone estimates in direct proportion. The air molecule scattering terms in the ozone estimates for double wavelength pairs, equations (1.10) and (1.11), are so small that they may, for convenience, be replaced by μh. However for single wavelength pair determinations, this substitution can be unsatisfactory, since the resulting percent ozone errors for the A, B, C and D bandpairs, respectively, are 0.2, 0.3, 0.5 and 1.0 times the percent difference between m and μh. For example, an error of about 1.5% could be expected for a single C bandpair measurement at an airmass of 3.8.
The ozone airmass μh depends on the mean height of the ozone layer. This varies over the range of about 13 to 30 km, but is usually between 17 and 27 km (Khrgian, 19751 WMO, 1981). It is highest and least variable in the tropics, and lowest and most variable at high latitudes and at high mid latitudes. It is now recommended by Komhyr (1980b) that approximate climatological mean layer heights be used for h in the computation of μh in order to avoid mean biases. The values recommended may be expressed as h = (26 - φ/10) km, where φ is the magnitude of the latitude. The effect of station altitude is not great since the highest stations are at about 3 km in altitude and most are below 1 km, but at the same time, it can be of significance for high airmass measurements and the altitude should be included in equation (12.4). The small variation of R around the globe has negligible effect on the accuracy of μh.
The dependence of μh on h-r is illustrated in Table 12.2 in terms of the percentage difference relative to the case of h-r = 22 km.
TABLE 12.2
Difference, in percent, of airmass at various
values of h-r, relative to h-r = 22 km.
h-r = 14 18 22 26 30 km
Z = 60° 0.4 0.2 0 -0.2 -0.4 %
75° 1.6 0.8 0 -0.8 -1.5 %
80° 3.4 1.7 0 -1.6 -3.1 %
83° 6.2 3.0 0 -2.7 -5.2 %
The table shows that if the value of h-r is fixed at 22 km, as was customary until recently (see Dobson 1957a), there will arise significant errors for high airmass measurements when the layer mean height is very high or very low. This is of particular significance for high latitude sites since these sites normally are subject to both low mean layer heights and high airmass values. Mid latitude sites are also affected in the winter since the zenith angle listed above, 60°, 75°, 80° and 83°, correspond to the noon airmass at winter solstice at latitudes of 37°, 52°, 57° and 60° respectively.
The use of the recommended climatological mean layer heights will significantly reduce the above mentioned error in climatological ozone data. However some error will remain owing to the uncertainty in the climatological mean layer heights, and to the correlation of ozone amount with layer height. Errors in airmass, and therefore ozone amount, due to day to day and seasonal variations in mean layer height may be estimated from Table 12.2. The sensitivity to such variations is approximately 0.05, 0.2, 0.4 and 0.7% km respectively at the zenith angles 60°, 75°, 80° and 83°. Since variations in mean height can be of the order of 2 km, day to day ozone errors of over 0.5% may be common for measurements made at airmasses over 4. The measurement types recommended (Komhyr, 1980b) for the higher airmass ranges, the CD focussed image and zenith sky measurement types, are those principally affected.
The sensitivity of airmass calculations to errors in timing of observations and to errors in the latitude and longitude assumed for a site may be readily found by differentiating equation (12.5). The percentage airmass error, εp, due to timing and longitude errors, at the times of the equinoxes, is given by:
εp = -100 tanθΔθ (12.6)
where Δθ (in radians) is the hour angle error or equivalent longitude or timing error. The airmass error is greatest at large hour angles and is independent of latitude for any given hour angle. The error values listed in Table 12.3 below show that in order to keep such errors below a few tenths of a percent, the timing of observations should be accurate to about 10 seconds, and the site's longitude should be accurate to about 2 minutes of arc, which is equivalent to a distance in the east-west direction of about 3.5 km at the equator. Similar east-west distance accuracies hold for higher latitudes also, owing to the compensation there of the smaller distance per degree of longitude by the generally smaller hour angles at which measurements are made. Note that systematic timing and longitude errors will tend to cancel in daily data which are the means of morning and afternoon observations taken at similar airmasses.
TABLE 12.3
Percentage airmass errors due to timing
or longitude errors, at the equinoxes, as a function
of hour angle θ.
Error Δθ (radians) = 2.91 x 10-4 2.91x 10-3 1.75 x 10-2
(deg. min.sec.) 1' 10' 1°
(time) 4 sec 40 sec 4 min
(distance atequator) 1.8 km 18 km 111 km
Sec θ = 2 θ = 60.0° 0.05% 0.5% 3.0%
3 70.5° 0.08% 0.8% 4.9%
4 75.5° 0.11% 1.1% 6.8%
5 78.5° 0.14% 1.4% 8.6%
The percentage airmass error due to latitude error, at the times of the equinoxes, is given by:
εp = -100 tanφΔφ (12.7)
where Δφ is the latitude error in radians. The airmass error therefore is greatest at high latitudes and is independent of hour angle. The errors listed in Table 12.4 below show that in order to keep the airmass error to less than a few tenths of a percent, the site's latitude should be accurate to about 5 minutes of arc for low and middle latitude sites, and to about 2 minutes of arc for high latitude sites.
TABLE 12.4
Percentage airmass errors due to latitude errors,
at the equinoxes.
Error Δφ = 1' 10' 1°
Latitude = 50° 0.03 0.3 2.1%
60° 0.05 0.5 3.0%
70° 0.08 0.8 4.8%
80° 0.16 1.6 9.9%
Modern surveying methods are well able to provide the latitude and longitude accuracies required, though this does not necessarily mean that all sites achieve these accuracies. Similarly, there are few places in the world where timing accuracies of 10 seconds are not possible, but this alone does not guarantee 10 second accuracies in routine operations.
12.3 Summary
(i) The airmass for ozone absorption, μh, depends on the altitude difference between the ozone layer mean height and the observing station, as well as on the solar zenith angle. Errors in the calculation of μh transfer to ozone estimates in direct proportion.(ii) Mean ozone layer heights range from about 13 to 30 km, are greatest in the tropics and in the summer and autumn, and are smallest and most variable at high latitudes and in the winter and spring.
(iii) Climatological average mean layer heights should be used when calculating μh. The mean height of 22 km traditionally assumed may give rise to ozone errors of typically up to -1% in the tropics and up to +5% in high latitudes. The errors are negligible up to an airmass of 2, but then rise rapidly.
(iv) Even when climatological yearly average heights are used, residual day to day and seasonal variations will give rise to errors of over 0.5% for airmasses over 4.
(v) Generally, since measurements at high airmasses are required only at high and middle latitudes, the airmass errors will amount to less than 0.5% in the tropics almost always, but may rise to a few percent at high latitudes, especially during winter.
(vi) The airmass appropriate to air molecule (Rayleigh) scattering, m, may be safely approximated by μh for any double wavelength pair ozone estimate, but the proper value is required for single wavelength pair ozone estimates above an airmass of 2.
(vii) Airmass errors due to observation timing errors and to site latitude and longitude errors vary, principally with airmass and latitude. Overall, they will be held to less than a few tenths of a percent if the observation times are accurate to 10 seconds and the site's latitude and longitude are accurate to 2 minutes of arc.
Return to Table of Contents
Forward to Solar Constancy