1.1 Purpose and scope
Ozone plays a key role in the photochemical processes of the atmosphere and is intimately involved in the chemistries of the high altitude air pollutants such as fluorocarbons. Its strong absorption of radiation of wavelengths less than about 300 nm provides a shield to the sun's biologically damaging ultraviolet radiation, and it is under the protection of this shield that most living creatures have evolved. Any long-term changes of ozone concentrations due to natural causes or increasing pollution would be of considerable importance to the biosphere and to the physics and chemistry of the atmosphere. A great deal of research has been undertaken, especially in recent years, to better understand the processes involved and the risks of changes, and it is toward this end that this series of WMO reports is directed.
The measurement of ozone is of course an essential element of the attack on the problem. The most basic of ozone measurements is the measurement of the ozone overburden, or ozone column amount (total ozone) made by the sixty or more Dobson instruments around the world. The Dobson network has been the prime source of our knowledge about the global, seasonal and synoptic variations of ozone in the Past, and it will continue in the future to provide a means for calibrating the developing satellite-based measurement systems and virtually the only records of sufficient length suitable for the analysis of long term trends.
This report aims to provide a thorough review of the error sources in the Dobson instrument's measurement of column ozone amount. It approaches the problem from the point of view of the physics of the measurement method rather than from the point of view of the statistics of collected data. Error sources associated with various physical factors, for example instrument stray light, or atmospheric scattering, are examined one by one, and quantitative estimates of error for operational conditions are made for each. The relevant literature is reviewed, though for many of the topics considered there is very little published material, presumably owing to the specialised technical character of the problems, and partly for this reason the author has in places drawn heavily upon his own unpublished and largely theoretical work. Actual measurements have been used whenever possible to verify theoretical models.
It is hoped that the review's emphasis on the underlying physical basis of each error source will provide a basis for further understanding, further experimentation, and eventually increased accuracies. The approach used does have some inherent limitations. In particular, some error sources may be badly overestimated or underestimated, and the net effect of the described errors for any particular instrument is difficult to assess owing to the wide variation in standards of instrument maintenance and calibration, the variety of operational conditions, and the lack of firm information on many of the error sources. The complement to the approach is the careful analysis of laboratory and field data by those experienced with the Dobson instrument and its measurements. No doubt some studies of this sort already exist in unpublished form. Perhaps this review will encourage their revision and dissemination.
Ideally, the accuracy of Dobson measurements of column amounts of ozone should be 1%. Some error sources can contribute errors of 20% or more on occasion, while errors of less than 1% may be important if their effects are additive. By comparison, extreme natural variations in ozone are roughly ±50% of the mean. There are practical limits to accuracy and error estimations of course, and it seems that any effort to push accuracy figures to ever-lower levels is usually confounded by the greater numbers of the smaller error sources, by greater uncertainty in the estimation of the smaller errors, and by complicated second order effects and interactions among the error sources. Of course the accuracy figure sought, or estimated, will depend on whether one is concerned with absolute accuracy, instrument intercomparability, or instrument repeatability.
Note that the review does not concern itself with the Umkehr method of measuring height profiles of ozone concentration used with the Dobson instrument. However, most of the error sources discussed do have a direct bearing on the accuracy of the Umkehr method, and it would be most desirable that their impact on it be studied more closely.
No study of the Dobson instrument such as this could fail to emphasize its indebtedness to the instrument's designer and exploiter, G.M.B. Dobson, FRS. His International Geophysical Year (IGY) instrument manuals (Dobson, 1957a, 1957b, and Dobson and Normand, 1962) have guided operational practice for over twenty years, and the original theoretical basis and physical design of the instrument (Dobson and Harrison, 19261 and Dobson, 1931) have stood the test of time for more than twice this period. These papers, together with his working papers in Walshaw (1975), show qualities of experimental ingenuity, scientific dedication, and attention to detail which all can admire. It is well worthwhile and very interesting to read through his papers, including tile history of his work at Oxford (Dobson, 1968) and his biography (Houghton and Walshaw, 1977), to see the extent to which an era of discovery about atmospheric ozone, and hence our own present knowledge, are so dependent on his work.
1.2 Theory of Measurement
Ozone is readily measured by means of its absorption of solar radiation in the 300 to 350 nm ultraviolet spectral region. The absorption changes rapidly across this limited region: it is so great at 290 nm that virtually no radiation of this wavelength penetrates to the surface of the earth, but at 310 nm it is only comparable in effect to Rayleigh scattering, and by 350 nm it is less than one hundredth the effect of Rayleigh scattering and so is of negligible effect (Figure 1.1). The choice of wavelength range in which to make measurements is dictated by the balance between ozone information content (decreasing wavelength) and transmitted energy flux (increasing wavelength), and in practice the principal ozone measuring bands are in the 305 to 315 nm range. The theoretical basis of the Dobson instrument's measurement method is given in Dobson and Harrison (1926) and Dobson (1931) and additional information may be found in Dobson (1957a) and Dobson and Normand (1962). Craig (1965, pp. 177 to 179) gives a particularly clear and succinct derivation of the measurement equations, and Khrgian (1975) discusses the theory as part of a detailed review of atmospheric ozone and of the history and practice of its measurement.
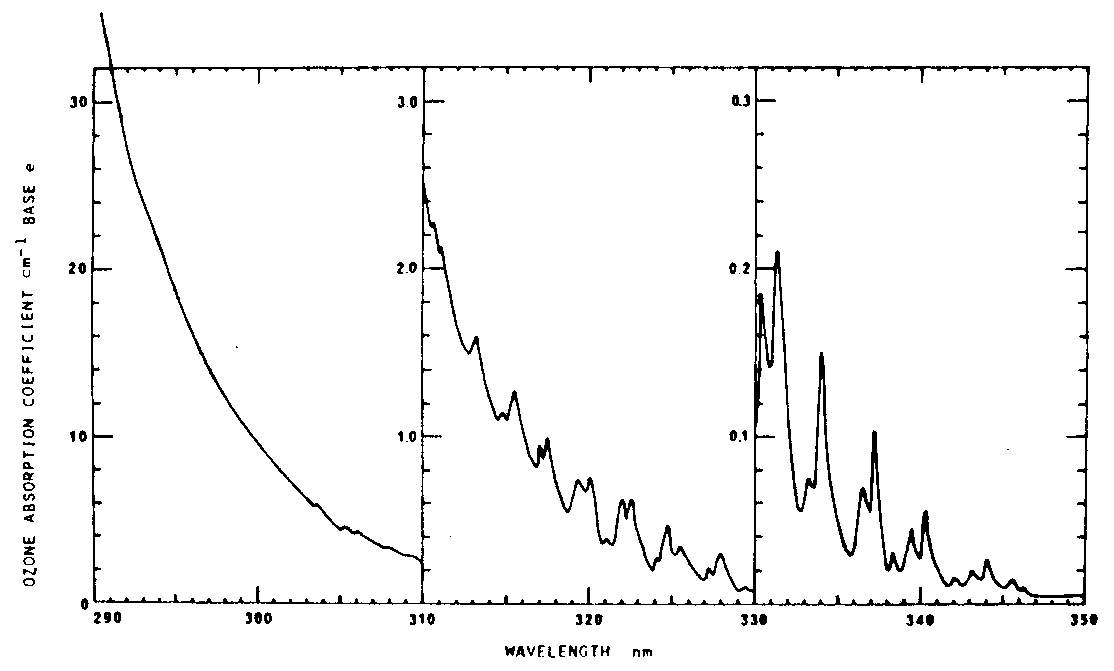
Figure 1.1: Ozone's absorption coefficient spectrum in the near UV at -44°C
(see Section 5.2 for source of data).
The measurement equation is found by calculus, with the effect of an infinitessimally thin layer of the atmosphere on a monochromatic band of direct sunlight being integrated with height front the earth's surface to the outside of the atmosphere. After some approximation of the integrals, the equation becomes, in simplest form,
log I(λ) = log I0 (λ) - μhXα(λ) - mβ(λ) - sec Zδ(λ) (1.1) where: λ = the wavelength of a monochromatic band. I(λ) = the intensity at the earth's surface. I0(λ) = the intensity outside the atmosphere. X = the vertically integrated amount of ozone, called the column amount of ozone or total ozone. α(λ) = the ozone absorption coefficient (to base 10) per unit of column amount. β(λ) = the Rayleigh (molecular) scattering coefficient for a vertical path. δ(λ) = the atmospheric aerosol scattering coefficient for a vertical path. μh = the secant of the solar zenith angle at the mean ozone height (usually assumed to be 22 km). m = the slant pathlength for air relative to a vertical pathlength and which accounts for atmospheric sphericity and refraction. sec Z = secant of the solar zenith angle at ground level. Note that, except when the sun is very low in the sky, the terms μh, m and sec are nearly equal. They are often collectively termed the "airmass" in this review.
A particular feature of equation (1.1) is its simple linear form. This greatly facilitates the manipulation and exploitation of the measurement method, as we shall see. For example, the Dobson instrument's measurement of two bands at wavelengths λ and λ', where λ < λ' can be described simply by the difference of two such equations, i.e. as:
I(λ) I0(λ)
log ------ = log ------- - μhX(α(λ)-α(λ')) - m(β(λ)-β(λ')) - sec Z(δ(λ)-δ(λ')) (1.2)
I(λ') I0(λ')
which is usually abbreviated to:
Lk = L0k - μh XΔαk - mΔβk - sec ZΔδk (1.3)
where k = A, B, C and D identifies the standard Dobson bandpair used. Equations (1.2) and (1.3) describe the measurement of relative intensity and they have three important advantages over the measurement of absolute intensity described by equation (1.1). Firstly, the stability and calibration of an intensity ratio poses many fewer problems than the stability and calibration of an individual intensity since it requires no absolutely calibrated reference source or detector and since many of the factors affecting stability, e.g. photomultiplier gain, will affect the two bands in equal proportion. Secondly, the variation in the intensity ratio is less than that of the individual intensities and therefore the dynamic range required of the instrument is less. Thirdly, because the average spectral gradient of Rayleigh scattering and aerosol scattering is much less than that of ozone absorption, the difference equations, (1.2) and (1.3), significantly reduce the contribution of the scattering components relative to that of the ozone absorption and therefore significantly increase the ozone information content.
The expression for column amount of ozone derived from equation (1.3) is:
L0k - Lk - m Δβk - sec ZΔδk
X = ------------------------------ (1.4)
μh Δδk
Most of the parameters required to solve the equation are readily determined: Lk is measured, μh, m and sec Z are calculated from a knowledge of the solar position at the time of the measurement, Δβk is found from scattering theory and is essentially a constant, and Δαk is found from laboratory measurements and is also essentially a constant. The standard coefficients used with the Dobson instrument are given below in Table 1.1. Note that the traditional unit of atm cm is used here and throughout the review. However, there is a good case for preferring the SI unit of mole per square metre as the unit for column amount of any atmospheric gas, and hence the mmol m-2 as the unit for column amounts of ozone (Basher, 1982a). In principle, the L0k term may be determined experimentally by exploiting the linearity of equation (1.3). A series of measurements of Lk for a clear half day is plotted against μh and extrapolated to find the intercept L0k at μh = 0. Equally well, equation (1.4) may be used, in which case the gradient of X against 1/&muhΔαk, where X is calculated with an existing or assumed L0k, gives the error in the L0k used. In both cases the atmospheric attenuation terms XΔαk, XΔβk and XΔδk must remain constant, but in practice this condition is often not met and such determinations of L0k are often unreliable. Increasingly, L0k are being found by the direct intercomparison of instruments against one of a few very well-calibrated reference instruments.
TABLE 1.1 Standard coefficients used with the Dobson instrument k A B C D Δαk 1.748 1.140 0.800 0.360 atm-cm-1 Δβk 0.116 0.113 0.110 0.104
It is worth digressing at this point to clarify the meaning of the term "extraterrestrial constant", since although this constant is indeed the quantity that is determined by the experimental methods described above, it is in fact not the same as L0k. Ozone measuring instruments like the Dobson instrument are not calibrated to measure intensities directly or even intensity ratios directly. Their output is an electrical or mechanical analogue:
P(λ) = C(λ) I(λ) (1.5)
where C(λ) represents the instrument's spectral responsitivity to I(λ) and is dependent on such things as slit widths and detector spectral sensitivity. The quantity measured by the Dobson instrument is therefore:
log P(λ)/P(λ') = log I(λ)/I(λ') + log C(λ)/(λ') (1.6)
= Lk + Kk
where Kk is a relative spectral response constant, dependent only on the instrument's design and adjustment. The extraterrestrial value, which is the extraterrestrial constant, is then:
Log P0(λ)/P0(λ') = L0k + Kk (1.7)
The extraterrestrial constant thus comprises an extraterrestrial intensity ratio, which is presumed to be a constant, and an instrument-dependent constant, which will vary among instruments and which will change with time as changes occur to, or are made to, the instrument and hence to its relative spectral response. The constants Kk are fairly small for Dobson instruments, but they may be large for other instrument types, depending on the instrument design. The stability of the Kk, but not the L0k, can be checked by reference to very stable incandescent lamps. This should be done both on a regular basis, and also before and after any adjustment or replacement of parts.
The final term in equation (1.4) to be discussed, and the most problematic, is the aerosol attenuation term Δδk. This term is very variable, owing to varying atmospheric conditions, and it is impossible to routinely estimate its size to sufficient accuracy by independent means. An ozone measurement made with only one bandpair is therefore an estimate Xk based on the equation:
L0k - Lk - mΔβk
Xk = ------------------ (1.8)
μhΔαk
which is related to the true ozone amount by the equation:
sec ZΔδk
Xk = X + ----------- (1.9)
μhΔαk
Equation (1.9) shows that the aerosol error component of Xk is airmass independent, since sec Z ≈ μh, and will tend to increase with decreasing Δαk, i.e., in going through the sequence k = A, B, C and D, owing to the l/Δαk weighting. The error for the C bandpair may reach ±15% on occasion (see Section 10).
The solution to the problem of aerosol error lies in the linear combination of the measurements of two bandpairs. If the two bandpairs are labelled k and j, then the difference of the equation (1.3) for each bandpair is formed and solved to give:
L0k - L0j - (Lk - Lj) - m(Δβk - Δβj) - sec Z(Δδk - Δδj)
X = ------------------------------------------------------------ (1.10)
μh(Δαk - Δαj)
As before, the aerosol component of the equation is unknown and the ozone estimate for the pair of bandpairs is:
L0k - L0j - (Lk - Lj) - m(Δβk - Δβj)
Xkj = --------------------------------------- (1.11)
μh (Δαk - Δαj)
which is related to the true amount by the equation:
sec Z(Δδk - Δ&deltaj)
Xkj = X + -------------------- (1.12)
μh(Δαk - Δαj)
The aerosol error component of equation (1.12) is much less than that of equation (1.9) for the single bandpair. This is due to the approximate equality of Δδk and Δδj, which is a result of the combination of the approximately linear spectral variation of aerosol attenuation δ(λ) in the limited spectral range of 305 to 340 nm and the similar wavelength separation of the bands within each Dobson bandpair.
The double bandpair method is the preferred method of ozone estimation, and the standard recommended bandpairs which are used are the A and D bandpairs. It can be noted that equation (1.10) increases the ozone information content by decreasing the relative size of the scattering terms, and will tend to reduce the effect of systematic errors in the L0 and L. Equation (1.11) can also be written as a weighted linear combination of the individual bandpair ozone estimates Xk and Xj, i.e., as:
Xk Δαk - Xj Δαj
Xkj = ------------------ (1.13)
Δαk - Δαj
This approach to aerosol scattering may be extended by explicitly expressing the scattering spectrum by an arbitrary polynomial and using the measurements of say n bandpairs to estimate the true ozone amount X and the n-1 coefficients of the polynomial. The set of simultaneous linear equations which result are of the same form as equation (1.9) and can be solved by standard matrix means, using the least squares method if only n-2 or fewer polynomial coefficients are sought. However, error anlyses have shown that, for various reasons, the linear polynomial is actually the most practical assumption, and hence that mathematical representations more sophisticated than equations (1.11) and (1.13) are not needed.
The theory of the preceding paragraphs describes the measurement of direct solar radiation when the sky is clear. When the direct radiation is insufficiently intense, or the sky is cloudy, it is possible to derive ozone estimations from measurements of the intensity of the blue, or cloudy, zenith sky, and such estimations form an important part of the available data archives. There is no simple theory to base them on, however, and instead they are found by means of their empirical relationship to the direct solar measurement type. The relationship is established over a period of time, sometimes years, by many sets of quasi-simultaneous measurements of the two types. The methods work reasonably well because, firstly, the light received from the zenith sky is scattered mostly at low altitudes, below the bulk of the ozone layer, and so experiences an optical path through the ozone which is similar to that of the direct beam, and secondly, the scattering by cloud water droplets has only a small spectral dependence.
Various assumptions have been made in the development of the above measurement theory and each may contribute some error to the ozone estimation. The important ones are listed at this point along with the section in which the relevant error sources are considered. It is assumed that the effect of other UV absorbers in the atmosphere, e.g., SO2, is negligible (see Section 11), and that atmospheric sources of radiation within the instrument's field of view, e.g., due to emission (see Section 11), or to atmospheric scattering (see Section 4), are also negligible. It is assumed that the means described above for dealing with aerosol attenuation are sufficiently accurate (see Section 10). It is assumed that the Rayleigh scattering coefficients are known to good accuracy (see Section 10), and that the ozone absorption coefficients are independent of atmospheric conditions and are also known to good accuracy (see Section 9). It is assumed that the extraterrestrial intensity ratio L0k is constant (see Section 13) and that the atmosphere is, on occasion, sufficiently stable to allow the determination of the extraterrestrial constants (see Section 7). It is assumed that the mean values of the slightly height dependent secant terms in the height integrals of absorption and scattering, in particular μh can be calculated to sufficient accuracy (see Section 12). Lastly it is assumed that the empirical clear and cloudy zenith sky measurements are valid (see Section 10).
1.3 Instrument design
A considerable amount of material describing many aspects of the Dobson instrument already exists (in particular, Dobson, 1931; Normand and Kay, 1952; Dobson, 1957a and 1957b; Dobson and Normand, 1962; Dobson, 1968; and Komhyr, 1980b), but for the sake of completeness and to emphasize those things relevant to this study of the sources of error, a brief description is given here.
The first instrument, number 1, was built by G.M.B. Dobson in his own workshop and is described by him originally in Dobson (1931), and also later in the historical review (Dobson, 1968). The historical review discusses the evolution of the design, and it shows how the 1931 design grew out of the previously available ozone measuring instruments and overcame their disadvantages. For example, it incorporated the good stray-light rejection and similar dispersive capability of the Fabry-Buisson double monochromator (see Figure 2 in Dobson, 1968), but by means of its mirrors M1 and M2 (see Figure 1.2) it halved the number of dispersive prisms required and folded the optical path to occupy a much more compact space. It also eliminated the need for the rather tedious photographic methods used with the Fabry-Buisson instrument and with Dobson's earlier Féry prism spectrograph, yet it exploited the optical wedge and photocell techniques developed by Dobson and his colleagues to analyse the photographic plates produced by the Féry spectrograph. It incorporated many other features, in particular, the AC amplification and null measurement method. The greatest significance of the instrument however, lay in it being the first instrument to give essentially instantaneous values of ozone amount and to be sufficiently straightforward to operate on a routine basis.
In subsequent years the instrument was commercially manufactured by R. and J. Beck Limited, and a number of improvements were gradually introduced, though it is a quite remarkable fact that the basic design, established in that short period before 1931, has continued virtually unaltered to this day. Perhaps the most important change was the use of photomultipliers from 1947 onwards, since these greatly increased the instrument's sensitivity and allowed the measurement of bandpairs at wavelengths shorter than the one bandpair at about 311.4 and 332.4 nm previously used. This in turn led to the discovery of the method of using two wavelength bandpairs to reduce aerosol effects. Of course, the electronics systems of most instruments have been continually upgraded, in line with technological developments.
Normand and Kay (1952) described the state of development of the instrument at that time, and succinctly summarised the principles of the design, adjustment and calibration of the instrument. Dobson expanded upon these, in preparation for the IGY, in his detailed instruction manuals for the instrument's operation (1957a) and adjustment and calibration (1957b). Later, Dobson and Normand (1962) gave a detailed discussion of the determination of instrument constants and of the accuracy of the ozone measurements under various conditions. Further studies by Dobson of the instrument's accuracy may be found in Walshaw (1975). The resurgence of interest in ozone in recent years and the consequent need to improve and standardize operational practice led to the publication in this WMO-Global Ozone Research and Monitoring Project series of an updated Operations Handbook prepared by Komhyr (1980b).
The essential features of the instrument are summarised in Figure 1.2 and are illustrated as follows by the passage of direct sunlight through the instrument. The light enters the prismatic sun director and is reflected downward through the lens to enter the main body of the instrument at the ground quartz plate (GQP). The prism and lens concentrate a rectangular swath of light on the GQP. The lens may also be adjusted to focus, with the GQP removed, a weak solar or lunar image directly onto the entrance slit S1. The GQP ensures a relatively diffuse, uniform and depolarised illumination of S1. The light from the GQP is reflected onto S1 by a small prism. The slit S1 is curved to correct for the instrument's greater dispersion of off-axis rays, and its width, along with those of slits S2 and S3, controls the spectral shape and energy throughput of the chosen wavelength bands.
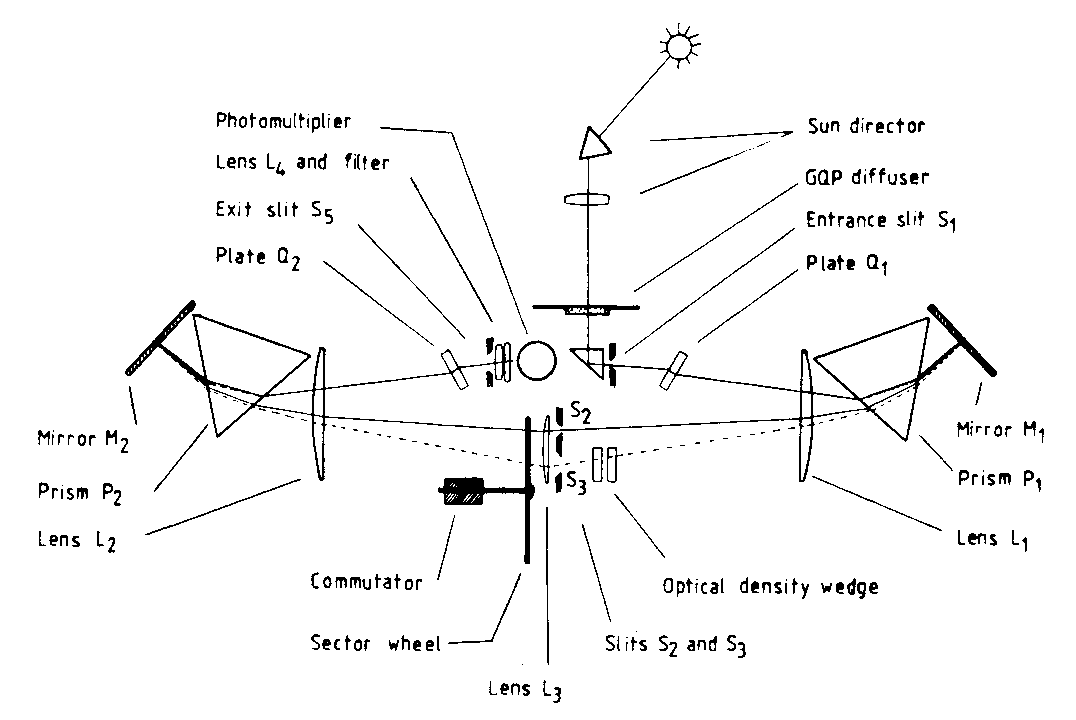
Figure 1.2 Schematic diagram of the main optical and mechanical parts of the Dobson spectrophotometer.
The light from S1 passes through the thick quartz plate Q1 and is corrected by lens L1, dispersed by prism P1, and in due course, focussed by L1 as a spectrum on the S2S3 slit plane. Plate Q1, when rotated, shifts the apparent position of S1, as seen at L1, and hence shifts the spectrum up and down at the S2S3 slit plane, thus allowing the selection of different wavelength bandpairs by S2 and S3, and also the correction of small temperature dependences. P1 is the instrument's principal dispersive element, and its top leading edge acts as a stop. Mirror M1 folds the beam back through P1 to double the instrument's dispersion, and its adjustment sets the initial wavelength position of the spectrum in the S2S3 slit plane. Slits S2 and S3 select the desired pair of wavelengths. The band transmitted by S2 has a wavelength in the 305 to 320 nm region, depending on the orientation of Q1, and a bandwidth of about 1 nm, and the band transmitted by S3 has a wavelength about 20 nm greater than that of S2 and a bandwidth of about 3 nm. The focal plane is actually not parallel to the slit plane but is oriented at about 55° to it. The focal plane is adjusted by means of L1 to coincide with S2 and hence to lie well behind S3. (Note that below S3 there is actually another slit, S4, which is not shown in Figure 1.2. A discussion of S4 and its associated components is omitted for brevity's sake.)
The optical density wedge device in front of S3 is used during a measurement cycle to attenuate the greater intensity of the longer wavelength band until it is registered by the null detection system (see below) as equal to the intensity of the shorter wavelength band. There are actually two wedges, which are simultaneously moved in mutually opposite directions (in and out of the plane of the diagram) by means of an externally mounted, manually operated mechanical dial. The dial must be calibrated in terms of the log intensity attenuation it produces.
The principal purpose of the right-hand half of the instrument is the selection of the desired bands, while the principal purpose of the symmetrical left-hand half is the rejection of the stray light in those bands. Light from S2 and S3 is directed by lens L3 towards lens L2 which collects it and focusses it via prism P2, mirror M2, and plate Q2 onto the exit slit S5. It is longer wavelength stray light in the short wavelength band that is the main problem, but the dispersion by P2 ensures that most of this stray light will be projected below slit S5 and will not be seen by the photomultiplier detector mounted behind the slit. There is also a filter at S5 which strongly absorbs stray radiation of wavelengths greater than about 400 nm. The lens L4 at S5 projects an image of P2 onto the detector so that both of the selected bands fall on the same area of the detector. The lens L3 projects an image of the top leading edge of P2 backwards via L1, P1, and M1, to lie between L1 and P1 and so form a lower stop acting on undispersed light, this stop being complementary to the stop formed by the top of P1.
The motor-driven sector wheel beside L3 is part of the null detection system. It is this system which tells an operator when his adjustment of the optical wedge has equalised the intensities of the two bands being measured. The wheel continuously rotates and alternately transmits the beams from S2 and S3, allowing them to alternately impinge upon the photomultiplier. The alternating component of the photomultiplier's output is amplified, and this in turn is rectified by the commutator which is mounted on the sector wheel shaft (or by means of an optical switch at the wheel edge) to give a DC current which is proportional to the difference of the intensities of the bands. The current is displayed to the operator by a meter. When the intensities have been equalised the meter reading is zero.
The main sources of error associated with the instrument itself are now listed, along with references to the Sections in which they are considered in more detail. Experience has shown that the accuracy of the instrument is less affected by fundamental design limitations than by inaccurate optical adjustment, (Section 2), wedge calibrations (Section 3), and extraterrestrial constants (Sections 5 and 7). Poor operational practice may also be a problem (Section 7). Among the more fundamental limitations are the sensitivity of the ozone measurements to the uncertainty in band centre wavelengths arising from normal calibration and operational practice (Section 5), the effect of finite spectral bands (Sections 6), mechanical and temperature stability (Section 2), the limitations of focussing, optical stopping and other optical peculiarities (Section 2), and the effect of stray light (Section 4). Various electronics problems may also arise (Section 8).
Note added in press
The wavelengths selected by slit S2 and S3 are usually assumed to be those listed for the standard A, B, C and D bandpairs in Dobson (1957a, p. 47), namely, A (305.5, 325.4), B (308.8, 329.1), C (311.45, 332.4) and D (317.66 and 339.8), all in nm. However, C.L. Mateer (personal communication) has pointed out that the A band 325.4 nm value is inconsistent with the other values and probably should be about 324.14 nm, the value listed in a less obvious table in Dobson (1957b, p. 110). If so, the resulting wavelength change would affect many of the calculations in this review, though only to a small extent.
Return to Table of Contents
Forward to Optics