4.1 Introduction
The term "stray light" is considered here in the wide sense as being any radiation which contaminates the radiation measurements defined by the equations of Section 1. It thus includes unwanted radiation scattered within the instrument and unwanted radiation scattered in the atmosphere and entering the instrument's field of view. A useful distinction can be made between homochromatic and heterochromatic stray light, the former being unwanted radiation of the same wavelengths as those of the bands being measured, and the latter being unwanted radiation of wavelengths outside the desired bands.
Strong evidence for the importance of stray light in the Dobson instrument can be found in Dobson and Normand (1962), Walshaw (1975), Basher (1978), and Olafson and Asbridge (1981a). Each of the particular instruments concerned shows the characteristic effect of ozone amounts apparently declining with airmass above an airmass of about 2.5 (e.g. as in Figure 4.3). For direct sunlight A or AD measurements, errors of 1%, 3% and 10% may be present at airmasses as low as 2.5, 3.2 and 3.8 respectively. For the C bandpair these errors occur at higher airmasses, perhaps at 4.5, 5.1 and 6.4 respectively. It is principally the addition of stray light to the shorter wavelength, and therefore the lower intensity band of a bandpair that is the problem. There appears to be a wide variation in the effect among instruments.
It is obvious that stray light will cause the greatest problems at high latitude sites. The general instruction in the WMO Operations Handbook (Komhyr, 1980b) is to limit the ordinary direct sun AD measurement to airmasses less than 3 and to use one of the less reliable or less accurate methods such as direct sun CD or focussed image AD types.
4.2 Stray light from atmospheric scattering
Radiation scattered by the atmosphere into the instrument's field of view contributes a stray light intensity which is approximately proportional to field of view and to airmass. This light contributes homochromatic and heterochromatic components and will include single and multiple scattered components. Its effect on the ozone measurement is usually negative but may be positive and will depend on the relative intensity of the bandpair's intensities, the amount of the scattering material, the material's spectral and angular (phase function) scattering properties and the optical depth along the beam's path.
Rayleigh scattering's inverse fourth power dependence on wavelength and broad cos2φ phase function results in a rather spatially uniform and bright (i.e. very hazy) sky radiance at 300-320 nm. Its main effect is the contribution of homochromatic stray light to the shorter wavelength bands and hence a reduction in the measured ozone amount.
The attenuation by aerosol scattering (due to particles typically from 0.05 to 5 µm in diameter) has a weak spectral dependence as discussed in Section 10, and a multi-lobed forward-peaked phase function. Both vary with the ratio of aerosol diameter to wavelength. Because of the strong forward peak, most of the scattered energy lies in the sun's aureole, i.e. within a cone of a few degrees around the sun and therefore within the Dobson instrument's field of view. The homochromatic component and the internally scattered heterochromatic component both serve to reduce the measured ozone amount.
The attenuation by individual cloud droplets (typically 10 to 1000 µm in diameter) is essentially spectrally uniform but colouring effects as shown by coloured rings about the sun and moon can arise owing to the dependence of the very strongly peaked and multi-lobed phase functions on the diameter/wavelength ratio and to internal reflection and refraction in the droplets. For all but the thinnest of clouds multiple scattering becomes dominant. The effect of these factors on stray light is unclear.
In Walshaw (1975) G.M.B. Dobson describes a detailed investigation of total ozone measurement errors when the sun is low in the sky. He shows that by using the Dobson instrument's sun-director lens to focus an image of the sun directly onto the entrance slit, instead of using the usual ground quartz plate diffuser, it is possible to extend the usable range of the C bandpair from an airmass of 4 to an airmass of 6. The limits are dependent on the actual amount of attenuation by ozone, and the advantage is gained presumably as a result of restricting the instrument's field of view. The WMO Operations Handbook (Komhyr, 1980b) recommends this focussed image method for the AD band combination for airmasses 2.5 to 4.0, and for the CD band combination for airmasses 2.5 to 6.0.
The focussed image method is not an easy one to carry out however, and there are two particular questions concerning its accuracy. Firstly, because the sun's image does not fully fill the length of the slit, errors will arise owing to the varying spectral sensitivity within the instrument's field of view (Basher, 1980; see also Section 2). Secondly, because the sun's image overlaps the width of the slit, errors will arise owing to the sun's limb darkening, i.e. to the relative richness of UV in the centre of the solar disc. In each case there will be a change in the extraterrestrial constants. Dobson (1957a) notes that there is a "small difference" in the constants, but Kulkarni (1968) found that for his instrument the difference was relatively large, at about 0.15, equivalent to a 40% increase in the ratio of the short wavelength intensity to the long wavelength intensity. It is quite clear that wherever the focussed image method is used, the size of the change in the extraterrestrial constants must be determined and if necessary applied as a correction. Brief mention of this need is made in the WMO Operations Handbook.
Dobson also describes (in Walshaw, 1975) a test to determine the "skylight" error, in which the sun's image is positioned firstly on the slit, and secondly just off the slit, and the error is estimated from the difference in the measurements. Presuming that other effects such as those described above can be neglected, the data shows the skylight error is equal to 1% in total ozone at an airmass of about 6.0 to 6.5 for all wavelength pairs. Correction procedures for both skylight and scattered light when the focussed image method is used are described by Hamilton (1964).
A computer modeling experiment to determine ozone errors due to atmospheric scattering was carried out by Thomas and Holland (1977). They used a Monte Carlo simulation of radiative transfer through an atmosphere of fifty 2 km layers which included a Haze-C aerosol size distribution of 0.11 decimal optical depth. Receiver instrument fields of view of 2°, 4°, 8° and 10° diameter were considered. They refer to a paper by Olafson (Ozone Symposium, Monaco, 1968) which indicates that an 8° diameter is appropriate to the Dobson instrument, presumably with the diffuser plate in place. The actual field of view at any time will depend on the fore-optics, such as the sun director, which are being used. For the 8° field of view, and at an airmass of 2, the proportion of single and multiple scattered radiation to attenuated direct radiation amounted to less than 1% for Rayleigh scattering and to about 2.5% for the aerosol scattering. The proportions increased with decreasing wavelength and increasing field of view. The ozone errors arising solely from this extra radiation received were less than 0.5% for single bandpairs and less than 0.2% for the double bandpair combinations. The calculations were limited to an airmass of 3, but extrapolation beyond this to an airmass of 4 suggests that there the errors for single bandpairs may be about 2%. This is a larger estimate than that given by Dobson's work and noted above, which may be due in part to the greater density of the aerosol model used by Thomas and Holland. The authors showed that the errors are approximately linearly dependent on aerosol amount. The aerosol optical depth of 0.11 used by them may be compared with visible (500 nm) optical depths of 0.02 for very clear conditions to 0.5 for extremely hazy conditions (Flowers et al., 1969). A value of 0.3 usually gives a milky sky in which clouds are difficult to discern. Note that Thomas and Holland's computations consider only homochromatic stray light.
4.3 Stray light from internal scattering
Radiation entering the Dobson instrument must pass through either twenty eight or thirty two optical surfaces and undergo three reflections before reaching the photomultiplier The possibility of undesired stray reflections is high, and since for quartz surfaces the reflection coefficient at 310 nm is about 3.8% for normal incidence, the energy involved in the stray reflections will be also high. In addition there will be present the usual optical aberrations of lenses and prisms, and finite slit widths, which will reduce the spectral purity of the instrument's images. Attenuation of short wavelength bands by poor quality quartz optics has been found to be associated with stray light problems (W.D. Komhyr, personal communication). Any such depletion will serve to magnify the effects of longer wavelength stray light.
Some of the stray radiation will be homochromatic but by far the more troublesome is the heterochromatic component, particularly from about 350 to 400 nm whose incoming energy in the direct beam is orders of magnitude greater than that of the narrow and highly-attenuated bands being measured. For example, for the 305.5 nm band at an airmass of 3 the incoming energy ratio is about 10+4 and hence the rejection of the stray radiation must be better than 10-6 in order to obtain an accuracy of 1% in the 305.5 nm band energy measurement. The second monochromator in the instrument is the essential means for reducing the effect of the heterochromatic stray radiation transmitted by slits S2 and S3. It casts a spectrum onto slit S5 such that, in principle, only radiation in the immediate vicinity of the desired bands is passed. An absorption glass filter at S5 removes radiation of wavelength greater than about 400nm. The effectiveness of the second monochromator depends on the nature of the spectra of light presented to it, as well as on its basic optical design.
Dobson (in Walshaw, 1975) examined the stray light spectrum transmitted by slit S2 by rotating mirror M2 and therefore sweeping the spectrum across the exit slit S5, and found a broad peak with half-intensity points at about 350 and 400 nm. He explained how a solution of nickel sulphate could act as a filter to this band, though this method is not now described as a recommended method in the WMO Operations Handbook, possibly because of the temperature dependence of the transmittance of the solution.
The writer had the opportunity to observe stray light directly within the prototype Dobson instrument, number 1, at Oxford, and was surprised to see reflected in lens L1 two bright white-light images of slit S1 and two less bright spectral images. A simple calculation shows that the ratio of this reflected energy transmitted by slit S2 to the energy in the 305.5 nm band is about 3 x 10-3 at zero airmass and about 2 x 100 at an airmass of 3. The 3 mm width of the S5 slit will accept a wavelength interval of approximately 8 nm in the vicinity of the 305.5 nm band and therefore might accept a not insignificant proportion of this stray radiation. The lens L2 will also directly reflect onto S5 a portion of the stray light transmitted by S2, but calculations show that the energy contribution is insignificant relative to that of the 305.5 nm band, even at an airmass of 3.
A second surprise was the realisation that the thick Q1 quartz plate, used mainly for the selection of wavelength pairs, creates a ghost image by internal reflection whenever it is aligned away from normal to the beam. This ghost reflection has an intensity of about 1.4 x 10-3 times the intensity of the main beam and is displaced from, but is nearly parallel to the main beam. Hence at the S2S3 slit plane there is a ghost spectrum, displaced in wavelength in the opposite direction to that of the wavelength pair selected. For example, the selection of the A bandpair will present at slit S2 the desired 305.5 nm band and a ghost band at about 323.8 nm. The energy contribution of the ghost image at S2 will be approximately 1%, 5% and 21% at airmasses of 1, 2 and 3 respectively. The second monochromator can be expected to reject most of this unwanted radiation, though its effectiveness will be limited by the quality of its optical adjustment and by the relatively broad 8 nm acceptance bandwidth of the exit slit S5. Note also that the second quartz plate Q2 will create ghost images at S5 of the S2 and S3 slits, and that for the A bandpair the ghost image of the 323.8 nm stray light will be aligned almost directly on S5.
4.4 Non-linearity of log intensity ratios versus airmass
The stray light contribution to the short wavelength band of a pair results in a non-linearity of the log intensity ratio versus airmass function. This gives rise to two errors, as is shown in Figure 4.1. The first is the obvious one of the reducing log intensity ratio and therefore reducing ozone measurement with airmass. A less obvious second error is the overestimation of extraterrestrial constant (ETC) that would be derived from the log intensity versus airmass data. This second error is a rather insidious one since the wrong ETC will make the ozone measurements appear more constant with airmass and the residual curvature in the data seem small, but at the same time it may be concealing a relatively large systematic negative error in the ozone measurements.
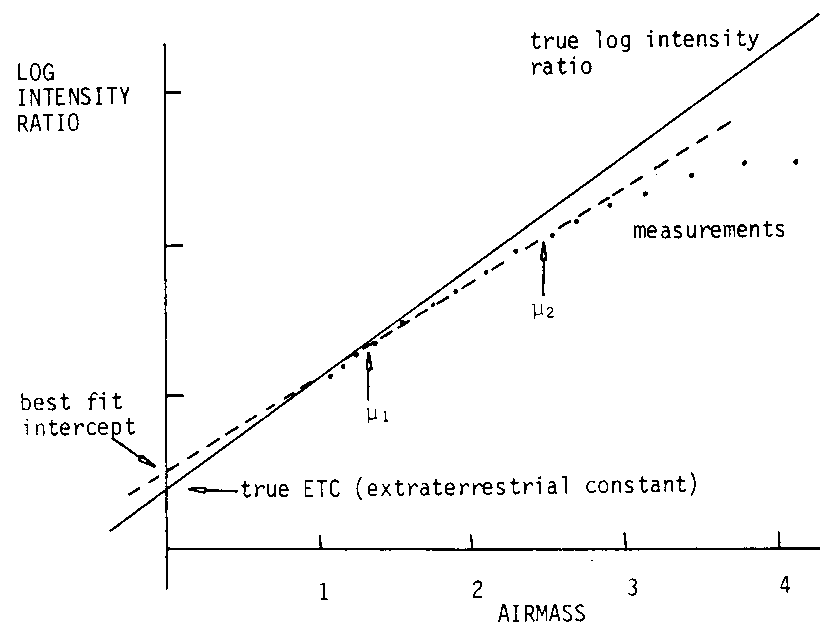
Figure 4.1 Illustration of the effect of stray light on log intensity ratios and on the determination of extraterrestrial constants.
Non-linearity errors have been investigated by the writer for a simple monochromatic, heterochromatic stray light model. The stray light is defined, firstly by R0, the ratio of the energy of the monochromatic stray light source to that of the desired band as would be measured under the imaginary conditions of zero airmass, and secondly by a, the atmosphere's relative attenuation coefficient of the stray light band to the desired band. If the stray light band was centred at 370 nm, corresponding to the centre of the band measured by Dobson (Walshaw, 1975), and the desired band is at 305.5 nm, then R0 would range from perhaps 10-5 to 10-3, depending on the quality of the instrument, and the parameter a would range from about 0.7 to 1.2, depending on ozone amount. The contribution of the stray light to the longer wavelength band of a pair, in this example the 325.4 nm band, is negligible, and the errors are not very dependent on the assumption of monochromaticity or centre-wavelength of the stray light band. The resulting equations for ΔETC, the error in extraterrestrial constant, and for ΔX the total error in the ozone measurement are:
1 (1 + R010μ2a)μ1
ΔETC = --------- log ----------------- (4.1)
μ2 - μ1 (1 + R010μ1a)μ2
-1
ΔX = ----- (ΔETC + log (1 + R010μa)) (4.2)
μΔα
where μ1 and μ2 are the airmass values at which
the straight line used to determine the ETC intersect the log intensity versus
airmass curve and Δa is the bandpair's ozone absorption coefficient.
A selection of results is given in Table 4.1 and Figure 4.2. In the calculation of the XAD ozone errors it has been assumed, for convenience only, that the relative attenuation, a, and therefore the ozone amount, is the same at the time of measurement as at the time of calibration of the ETC, and that the error source affects only the A bandpair. Attention is drawn to:
(i) The dependence of the ETC error, and therefore any ETC determination, on the airmass range used, and on the value of the parameter a, and therefore on the ozone amount. This may be a main cause for the difficulty of obtaining consistent ETCs for an instrument and for the lack of agreement between independently calibrated instruments.(ii) The relative uniformity of the ozone error in the operating range of 1 to 3 in airmass, and the way this tends to conceal what may be a significant underestimation of ozone amount.
(iii) The increased error at low airmasses, which is principally due to ETC error. In middle latitudes this will result in noon values that in summer are lower than morning and afternoon values, and that in winter are higher. This sort of behaviour has been observed in the Wallops Island Dobson instrument data (Geraci and Luers, 1978).
(iv) The strong dependence of the error on the parameters R0, a, μ1, and μ2. An instrument whose R0 is 10-4, might agree very well with another instrument whose R0 is 10-5 during a summer intercomparison when the ozone level is low, i.e. when a is about 0.8, but it would disagree by 5% or more under winter-spring high ozone conditions.
The measurements of any instrument can be compared to the calculated values to estimate the stray light levels present. The fact that for most Dobson instruments the XAD measurement is not satisfactory beyond an airmass of 3 suggests that Ro is typically about 10-4. The writer made measurements of XAD beyond this airmass using the Wallops Island Dobson instrument in 1977, and the average of the results for a range of ozone values is compared with two models in Figure 4.3. It suggests that the instrument's R0 value at that time, was about 10-3.8 to 10-3.6. The data of Figure 4.2 show that a value of 10-5 is the maximum desirable value. The airmass dependences shown by Olafson and Asbridge (1981) indicate that the Canadian No. 77 instrument is of this higher quality, which in turn indicates that the goal of R=10-5 is not unattainable.
TABLE 4.1 Errors in the determination of extraterrestrial constants for various stray light error models. Airmasses R0 = 10-5 10-4 10-4 10-4 10-3 m1 m2 a = 1.0 0.8 1.0 1.2 1.0 ------------------------------------------------------------------------- 1.25 2.0 ΔETC = .0003 .0012 .0035 .0094 .0327 1.25 2.5 = .0008 .0024 .0083 .0264 .0724 1.25 3.0 = .0021 .0050 .0200 .0717 .1440 1.25 3.5 = .0053 .0102 .0471 .1640 .2417 1.25 4.0 = .0137 .0209 .0998 .2870 .3414
Figure 4.2 Variation of zone error XAD as a function of airmass μ, for various values of model parameters, as calculated by the stray light model.
Figure 4.3 Comparison of experimental data with stray light models: (_____) R0 = 10-3.8 a = 1.0 μ1 = 1.0 μ2 = 2.5 (-----) R0 = 10-3.6 a = 1.0 μ1 = 1.0 μ2 = 2.5 See text for details.
4.5 Possible solution to stray light problems
Up until now very little attention has been given to the question of stray light in the Dobson instruments. However, there is every indication from the above studies that it is one of the most important sources of ozone measurement error, and it is highly desirable that suitably equipped laboratories with Dobson instruments begin to study directly the origins and transfer of stray light in the instrument, both theoretically and experimentally. Of particular interest are the direct reflections from lens L1, and the ghost image spectrum from plate Q1 . Simple optical stops may be a solution. Olafson and Asbridge (1981a) describe an alteration to the orientation of Lens L1, which serves to increase the usable airmass range for the A bandpair from 2.5 to 3.5, presumably as a result of stray light reduction. Some of the stray light problem simply may be due to a poor quality of quartz in the optics, or to poor adjustment of the instruments of course.
As was pointed out above, it is possible to test for stray light by taking measurements out to high airmass and comparing the results with a stray light model. Another method, which has been used very successfully by the author to detect a long wavelength leakage band in a faulty UV interference filter, is to use soda glass plates to selectively block out the desired UV band in favour of the undesired stray light band. Measurements are made by successively adding from one to six or more plates of about 7 mm thickness to the optical path. If the A bandpair is being measured, the main 305.5 nm band is virtually eliminated by the time two or three plates are added and successive plates then give rise to a log intensity ratio versus plate number function that depends only on the 325.4 nm band and the stray light band, and is nearly linear. The intercept at zero plate number gives the "extra-terrestrial" energy ratio of the stray light band relative to the 325.4 nm band, and the slope will indicate the mean wavelength of the stray light if the glass spectral transmission is known. The experiment can also be done as a function of airmass. Preliminary experiments with Dobson instrument number 1 were carried out by the author at Oxford in 1978, but owing to a lack of dynamic range and sensitivity in the instrument's detection system, they met with little success. Additional neutral density filters would be needed to reduce the relative intensity of the 315.4 nm or other shorter wavelength band, and one of the modern, sensitive detection systems now being used in Dobson instruments probably would be needed also.
4.6 Summary
(i) There is strong evidence of the effects of stray light on the Dobson instrument. It is a major error source and it sets a major limitation to the instrument's operating range, typically at an airmass of about 3.(ii) The errors due to homochromatic stray light scattered by the atmosphere into the instrument's field of view appear to be on average no more than 1% at an airmass of 3. The error is approximately proportional to aerosol amount and field of view and it increases with airmass.
(iii) The focussed image method can extend the instrument's operating range of airmass, presumably owing to its restriction of the field of view. It will result in changes to the extraterrestrial constants however, and these changes must be determined and corrected for.
(iv) Heterochromatic stray light, in the 350 to 400 nm wavelength region, undoubtedly the most troublesome form of stray light. A white light reflection from lens L1 and a ghost image from quartz plate Q1 are important candidate sources. Other sources may be present, including some dependent on the instrument's optical quality and quality of adjustment.
(v) A model of heterochromatic stray light shows that the resulting ozone measurement errors can be large yet may remain undetected. The errors are very dependent on the model conditions, and will vary widely among different instruments and under different operating conditions.
(vi) Insufficient is known about the details of stray light propagation in the instrument and how to avoid its effects. Further study is most desirable.
Return to Table of Contents
Forward to Wavelength Band Uncertainty