2.1 Introduction
The Dobson instrument has the character of a laboratory instrument even though it is used in routine outdoor use, and its adjustment and maintenance requires a relatively high level of skill and technical knowledge. For example, the widths of slits S1 and S2 must be set to an accuracy of 0.4 ±0.01 mm, which gives a bandwidth accuracy of 1.0 ±0.025 nm, and the tilt angle of mirror M1 must be stable to a precision of about 9 x 10-6 radians or 1.9 seconds of arc to provide a wavelength accuracy at S2 of 0.025 nm. Other problems to be overcome are: the physical confinement of some of the components which have to be adjusted, the temperature dependence of some adjustments, and the fact that alignments and focussing must be done for ultraviolet light which, of course, is not visible to the human eye.
Detailed methods for the instrument's adjustment are given in Dobson (1957b). It is now generally accepted and recommended that these adjustments should be attempted only by skilled technicians (Komhyr, 1980b), and preferably only with the guidance and assistance of WMO or of those experienced and expert in these adjustments. It is important to note that although the instrument in principle can be made to operate satisfactorily wider a variety of adjustment regimes, the necessary intercomparability of instruments demands that all instruments in fact use a common set of wavelengths and transmission band shapes and therefore be adjusted and calibrated in a uniform fashion to common standards.
2.2 Optical adjustment
The main objectives of the adjustments specified in Dobson (1957b) are to ensure that the alignment, stopping, focussing and wavelength band selection of the instrument are properly set. The general effect of inadequate adjustments are as follows. Poor alignment of the optical components can cause many problems, including defects in optical stopping, increased effects of optical aberrations, increased stray light and decreased sensitivity. Defects in stopping, which can also arise from an incorrect focal length of lens L3, cause the instrument to have a varying spectral sensitivity for light near the edge of the field of view (Basher, 1980). Improper focussing of lens L1 results in a broadening of the wavelength bands, particularly those transmitted by slit S2, and excessive effects of lens aberrations. Errors in the focussing of lens L2, in the adjustment of plate Q2 and in the width of slit S5, can reduce the sensitivity of the instrument, can alter the relative spectral sensitivity, and can increase the effect of stray light. Errors in the adjustment of mirror M1 and plate Q1, and in the positions of slits S2 and S3, will cause errors in the centre wavelengths of the desired bands, while errors in the width and parallelness of the slits S1, S2 and S3 will cause errors in the shape of the bands.
The effect on ozone measurements of the residual uncertainty in the effective centre wavelength, width and shape of the transmitted bands arising from normal correct adjustments is considered in more detail in Section 5. The effects of stray light are discussed and estimated in Section 4. Error estimates are generally not available for the other uncertainties of adjustment, and it would be very difficult to estimate the size and behaviour of errors arising from abnormal and poor adjustments.
Gross faults in the optical system have been found on occasion (Komhyr, 1980b). These are such things as lenses of the wrong focal length, optical components made of material which are poor transmitters of ultraviolet light (e.g., crown glass), poor quality quartz glass, mechanical overtightening and stressing, looseness and slippage of parts, objects obstructing the optical path, oily or dirty optical surfaces, and mechanical delamination of the optical wedges found in early instruments.
The results of the intercomparisons of Dobson instruments listed in WMO (1982) give some idea of the possible limits of error due to poor adjustment. The early intercomparisons show differences of up to 10% for instruments which have been independently adjusted and calibrated, whereas instruments which have been more recently adjusted and calibrated by direct intercomparisons, and then intercompared a year or two later, generally agree to better than 2%. These error figures also include errors due to wedge calibrations and extraterrestrial constants. Ozone errors due to poor adjustment will tend to be dependent on operating conditions, particularly airmass, and therefore will tend to be very variable and may severely limit the operating range of an instrument.
The steady improvement in the results of the intercomparisons is in large part due to the systematic and rigorous test and adjustment procedures and instrument modernisations which are often carried out just prior to the field intercomparisons. WMO has sponsored much of this work, and with a view to its further encouragement and coordination, has recently designated the United States National Oceanic and Atmospheric Administration's Air Resources Laboratory in Boulder, Colorado as the World Dobson Spectrophotometer Central Laboratory. The data in WMO (1982) indicate that at least fifty instruments have been upgraded and calibrated, which is well over half of the network. It seems likely that most of these have intercomparabilities near the 2% level for ordinary direct sun observations with the AD bandpairs, and therefore errors due to deficient optical adjustment of less than 2% for such measurements.
2.3 Fundamental optical limitations
Dobson (1931) and Normand and Kay (1952) discussed the fundamentals of the instrument's optical design, but since then there has been no comprehensive study of its optical characteristics, for example, as might be done by computer ray tracing techniques. Bearing in mind the current demands for better accuracy and the known existence of certain optical problems, as detailed below, it would seem now timely for such a study to be undertaken. Two particular matters which require further investigation are, firstly, the aberrations of simple lenses (e.g. chromatic aberration, spherical aberration, astigmatism, etc.) and their effect on focussing and wavelength band definition, and secondly, the reflection of light from optical surfaces and its contribution to stray light in the instrument.
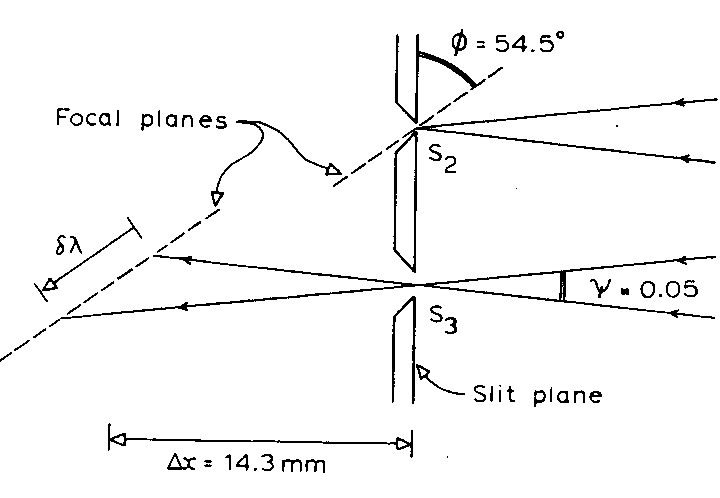
It was pointed out by Dobson (1931) that the instrument's focal plane is inclined to the slit plane. This problem was circumvented in the 1931 design by first ensuring a focus at slit S2 and then using auxiliary lenses on either side of S3 (and S4) to bring the longer wavelength bands to focus. However, in the later multi-wavelength design described by Normand and Kay (1951) and Dobson (1957a) the lenses adjacent to the S3 slit were omitted and only those near S4, the "achromatising" lenses, were retained. Basher (1980) found that the inclination angle is 55° and that if a sharp focus is present at S2, then the focus at S3 lies about 14 mm behind the slit.
About 4 mm of the focal error is due to the extension of the focus by the optical wedge, since flat plates extend focal lengths. The plate Q1, also extends the focus of both wavelengths, and since the extension is proportional to plate thickness, the focus for both will vary as the plate is rotated away from the normal to the beam. When the rotation is such as to choose shorter wavelength bands, the focus extension will partly compensate for the reduced focal length of the shorter wavelengths, but when the longer wavelength bands are chosen the extension of focus exacerbates the existing lack of focus.
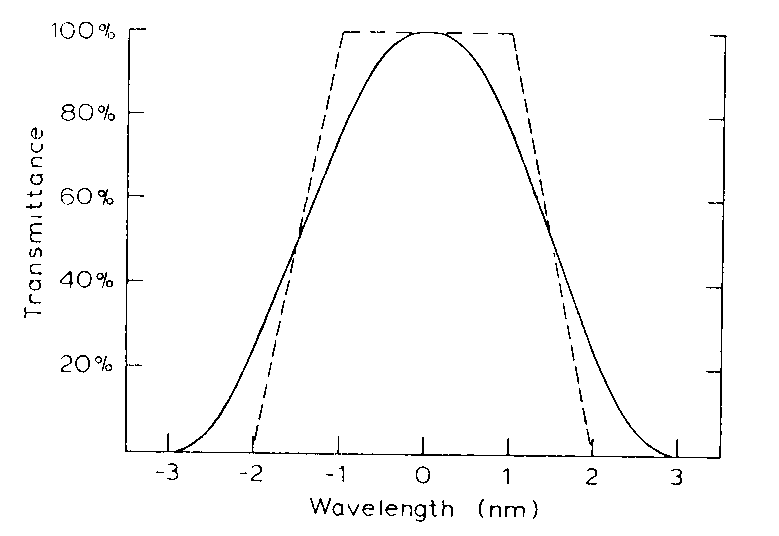
Two effects of the lack of focus at the S2S3 slit plane were discussed by Basher (1980). One is the greater spread of wavelengths transmitted by the slit and hence a smearing of the slit transmittance function and an alteration of the band's ozone absorption coefficient (see Figure 2.1). Fortunately it is the longer wavelenqth bands which are most affected and their absorption coefficients' accuracy has only a small effect on the ozone estimation accuracy. Preliminary measurements of the transmittance spectra of the World Reference Dobson Spectrophotometer No. 83 have been made recently by W.D. Komhyr (personal communication). The calculated spectrum in Figure 2.1 is in good general agreement with these measured spectra.
The other, and more important effect is the dependence of the transmitted wavelength on the incidence direction within the internal field of view as illustrated in Figure 2.2 (where this field of view is defined by the stops and not the GQP diffuser). The calculated shift in the S3 band's centre wavelength in traversing the field of view is about 2 nm. This means that the instrument's spectral sensitivity will vary across the field of view, with a log I/I' measurement varying by about 0.030 for an incandescent standard lamp, and by possibly up to 0.075 for solar irradiance. This appears to be the explanation for the "directional effect" described by Dobson in Walshaw (1975). It will cause significant problems when the light distribution within the field of view is variable, in particular, when an image of the sun or moon is focussed on the entrance slit.
It can be noted here that a further change in the Lo value appropriate to the focussed solar (but not lunar) image will arise owing to the solar limb darkening and its spectral dependence. As an example, at three quarters of the solar radius the intensity at 322 nm has dropped to 70% of that at the disc centre (see also Moe and Milone, 1978). Computations by Svensson (1958) of LoA, LoC and LoD for the case of a solar eclipse suggest changes in Lo of the order of 0.010. Focussed lunar images may have LO values different to those for sunlight, to the extent that the moon's reflectivity is not spectrally constant.
The effects of reflections within the Dobson instrument are not well known. A beam of light entering the instrument must pass through about thirty optical surfaces before reaching the detector, and since the reflectivity of the air to quartz interface at normal incidence at 310 nm is about 3.8%, there is a considerable amount of energy in the reflected light. The relative amounts of reflected and refracted energy at an interface depend on the incidence angle and polarisation of the beam. The GQP diffuser provides a well scattered and well depolarised light, and Dobson (Walshaw, 1975) found no noticeable effects from the variation of polarisation of natural skylight. However, when the GQP is not present there will exist the possibility of large error if the source of light projected onto the entrance slit has large or varying polarization. It is possible that the large variation in relative spectral response found by Dziewulska-Losiowa (1978) when using a polaroid film at varying orientation arose as a result of the GQP being absent. (The film has potential for reducing ozone errors in cloudy conditions - see Section 10).
Reflected energy contributes to the instrument's stray light problem, which in turn limits the effective dynamic range of the instrument. Two particular optical problems noted by the author and discussed below are the internal reflection of light in plate Q1, and the direct reflection of light from slit S1 onto the S2S3 slit plane by lens L1. Of course there may be other similar problems awaiting discovery.
It can be shown that when a tilted, thick flat plate like Q1 is used to displace a beam to one side of an optical axis there will be produced by internal reflection a second beam of reduced intensity which is displaced to the opposite side. In the Dobson instrument this produces a displaced "ghost" image of the entrance slit S1 and hence a displaced "ghost" spectrum at the S2S3 slit plane. The intensity of the ghost spectrum is about 0.14% of the intensity of the main spectrum. It results in a significant stray light level at the S2 slit when the Q1 plate is tilted to select short wavelength bands since the ghost band is then shifted in the opposite direction, to longer and therefore more intense wavelengths bands. The author calculates that when the A bandpair is selected, the ghost band at S2 is centred at about 323.8 nm and its energy contribution at an airmass of 3 is about 20% of that of the desired 305.5 nm band. The stronger atmospheric attenuation of the 305.5 nm band thus serves to magnify the effect of the ghost band as the airmass increases.
The faces of lens L1 reflect white light from S1 directly onto the S2S3 slit plane. It is possible to calculate approximately the energy contribution of this light relative to that of the desired short wavelength band from a consideration of the reflectivity of quartz, the relative solid angles subtended by the sources, and the relative atmospheric attenuation. The "white light" detectible by the instrument can be assumed to lie in the range 380 ±40 nm. The author calculates that at an airmass of 3, the energy of the reflection transmitted by S2 is perhaps twice that of the band being measured.
It is therefore clear that the role of the second monochromator in rejecting stray light is a very important one, and that the adjustment of this monochromator deserves special attention. The rejection is to a large extent effective, but it is limited: by intrinsic focussing deficiencies, by the relatively broad 3 mm slit width of S5, which is equivalent to a 8 nm acceptance band, and by the rapid relative increase of the stray light with airmass. Komhyr (personal communication) reports that a characteristic of those well adjusted, well calibrated instruments which exhibit severe internal light scattering, is light attenuation at the short wavelengths by poor quality quartz optics, particularly prisms. Further discussion of the effects of stray light is given in Section 4.
Temperature affects the Dobson instrument's optics directly through the temperature dependence of the refractive indices of the prisms, lenses and flat plates, and indirectly by the distortion of the optical path imposed by differential thermal expansion. The temperature dependences of the optical components can be calculated from textbook formulae and data, such as is given in Basher (1980), and knowing the temperature dependence of the refractive index of quartz to be about 10-5 °C-1. It turns out that only the prism's dispersion dependence is of importance.
The instrument's temperature dependence is corrected for by small changes in the orientation of the Q1 plate, the required changes being determined by earlier experiments using line sources over a range of temperatures. Dobson (1957b) gives some results in the range of about 0.1 to 0.2 °Q/°C (where °Q refers to the angle change of the Q plate in degrees). Since the centre wavelength dependence on the Q1 angle, dλ/dQ, is about 0.2 nm °Q-1, the centre wavelength dependence on temperature is about 0.02 to 0.04 nm °C-1.
To provide a centre wavelength accuracy of 0.025 nm, which is very desirable (see Section 5), it is necessary, therefore, to ensure:
- that the temperature corrections are made for every 1°C change in temperature;
- that the temperature in the vicinity of the prism and the thermometer is uniform to better than 1°C;
- and that this temperature changes by less than 1°C during any single sequence of measurements (i.e., over one or two minutes).
To ensure a rigid instrument, free from the effects of mechanical deformation, the body is constructed of two boxlike halves bolted together, each half made of a single casting in aluminium alloy. It sits on three legs, to avoid the distortion which can occur with four legs. Mechanical stress due to people leaning on the instrument or resting objects on it may possibly have significant effects and should be avoided. Asbridge (personal communication) reports that distortions can arise if the gasket between the instrument's halves is very compressible and the tightening of the bolts is consequently uneven. The distortion in the instrument concerned was detected by means of wavelength checks with a mercury line source before and after assembly of the instrument. Incompressible spacer washers were used on some bolts to overcome this problem.
An approximate estimate of the effect of thermal expansion may be made as follows. Let us assume a temperature gradient from the top to the bottom of the instrument such that the top is 1°C hotter than the bottom, and a coefficient of expansion for the alluminium alloy of 1 x 10-5 °C-1. The resulting angular displacement in the vicinity of the prism P1 then would be approximately 500 x 10-5/200 = 2.5 x 10-5 radians, where 500 mm is the length of the right-hand half of the body and 200 mm is the height. This figure of 2.5 x l0-5 is larger than the figure of 9 x 10-6 needed to maintain the centre wavelengths to an accuracy of 0.025 nm, which would suggest that temperature differences across the instrument should be kept to less than about a quarter of a degree celsius, and that, quite possibly, thermal expansion stresses may contribute significant error on occasion. However, this is a very approximate calculation and the topic requires further study and experimental investigation.
The effective refractive index of quartz is slightly pressure dependent. Normand and Kay (1952) give the required correction of Q plate angle as one-half degree per 100 mb, which is equivalent to a centre wavelength change of about 0.1 nm per 100 mb. Atmospheric pressure changes at any site usually are within the range of ±30 mb, but on occasion can be ±50 mb, and so corrections for these changes are generally not attempted. However corrections are required if an instrument is shifted in altitude after a calibration has been done (see Komhyr, 1980b, p. 73).
Dobson, in Walshaw (1975), points out that moisture condensing on optical surfaces can be a problem. The dish of silica gel in the instrument will generally avoid any problems, provided it is kept replenished with fresh (blue) silica gel. Dobson reports that in one case when calibrating a wedge, it was necessary to change the silica gel every second day in order to get consistent calibration data.
The ultraviolet light within the instrument could induce fluorescence, and therefore stray light, if fluorescent materials such as paper, certain cloth, or lint or dust derived from them, are present. There is no information on this in the literature on the Dobson instrument, and it is probable that it is not a significant problem.
2.4 Summary
(i) The Dobson instrument is a precision optical instrument and its optical adjustment should be attempted only by skilled technicians trained for the task.(ii) Inadequate adjustment causes, principally, increased wavelength band uncertainty, increased stray light, and varying spectral sensitivity. It is virtually impossible to reliably assess the quality of a particular instrument's past adjustments and the errors associated with them. Uncertainties remaining after a correct adjustment are discussed in Section 5.
(iii) Experience indicates that poor adjustment has been an important source of error in the past. On occasion, gross optical faults have been found.
(iv) Intercomparisons have shown that, in the past, independently adjusted and calibrated instruments could differ by 10% in their measurements, but that recently adjusted instrument calibrated against a reference instrument generally differ by less than 3%. The improvement is largely due to the intercomparisons and the accompanying efforts to upgrade instrument optics, electronics and calibration.
(v) A number of fundamental optical problems have been identified, as noted in items (vi) and (vii) below. These point to the need for a comprehensive study of the instrument optics, for example by computer ray tracing methods.
(vi) The inclination of the focal plane smears the transmittance band functions and gives rise to the "directional effect", the varying spectral sensitivity across the internal field of view.
(vii) The multiple reflection of light in the Q1 plate, and the direct reflection of light from lens L1, contribute significant amounts of stray light to the shorter wavelength band. It is very important that the second monochromator be properly adjusted to effectively reject as much of this stray light as possible (see also Section 4).
(viii) Focussed image method ozone measurements are affected by the "directional effect" (possibly by up to some tens of percent, depending on the bandpair used), and by the solar limb darkening effect (possibly by up to 2%), or the lunar spectral reflectivity variations (possibly by up to 2%).
(ix) The temperature dependence of the wavelength bands is significant. This requires an internal temperature uniformity of 1°C or better, and the correction of wavelength settings at at least 1°C intervals.
(x) Mechanical deformation of the instrument can cause wavelength band errors. Temperature gradients across the instrument can cause deformations and may possibly be a problem.
(xii) Wavelength setting corrections are required when instruments are shifted in altitude, owing to a pressure dependence. A dessicant is required inside all instruments to prevent condensation on optical parts. Fluorescence inside the instrument does not seem to be a problem.
Return to Table of Contents
Forward to Wedge Calibration