3.       WEDGE CALIBRATION

3.1      Introduction

          The optical density wedge has a pivotal role to play in the Dobson instrument, and the accuracy of its density calibration is crucial to the accuracy of the ozone estimations. Originally, Dobson (1931) confidently assumed the wedge density to be essentially linear with wedge length and determined the density gradient by reference to a metal gauze of known transmittance. Subsequent experience, however, showed that linearity could not be assumed and that more sophisticated calibration methods were necessary (Normand and Kay, 1952, Dobson, 1957b, Walshaw, 1975).

          The first density wedges were constructed from gelatin containing carbon black sandwiched between two quartz plates, but these were found to be subject to delamination and mould growth on the gelatin. Evaporated metal films were later developed which had sufficient linearity (Dobson, 1968). Note that the wedge device consists of two individual density wedges. Komhyr and Grass (1972) reported that the Canada balsam cement which joined the two quartz plates of each wedge was not stable in transmittance. They described a better joining method which had given very good constancy in spectral transmittance over a period of more than ten years in the wedge of instrument number 83. (This instrument is now designated the World Primary Standard.)

          In principle, the wedge could be calibrated independently of the Dobson instrument, but in practice it is more accurate to calibrate it in situ, i.e., in the same configuration as is used operationally (Normand and Kay, 1952). Because the instrument's electrical response to intensity is not linear, the wedge density cannot be measured directly. Instead, the null detection system is used to obtain the change in wedge position, ΔR, as measured by the angle R of the external dial, that is needed to balance an applied and known change in intensity at the S3 slit, relative to a temporarily fixed intensity at either S2 or S4. The log of the intensity ratio for the change is then equal to the wedge density interval ΔD required to balance the change. A measurement sequence usually consists of a set of ΔR measurements as a function of R, such as is shown in Figure 3.1.

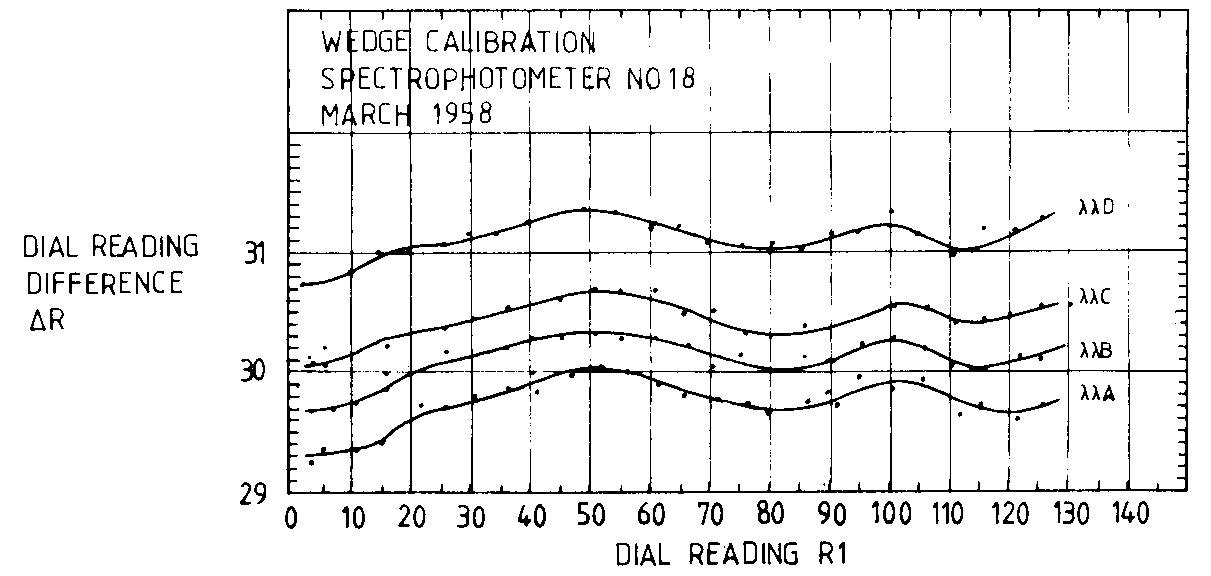
Figure 3.1 

Figure 3.1  Dobson optical wedge calibration data using the two lamp method
            (data from Komhyr, 1980b).

          In essence, the calibration of the wedge consists of, first, the measurement of the coarse density gradient ΔD/ΔR as a function of dial angle R, and second, the integration of this gradient with respect to R to obtain the density function D(R). The unknown constant of the integration forms part of the instrument's extraterrestrial constant which is determined by independent means (see Section 7). However, in practice, a more elaborate analysis procedure involving the "minor interval" method is used to calibrate the wedges.

3.2      Apparatus

          The most common means for providing known changes of intensity are the two-source intensity doubling or halving devices, in which two sources of closely equal intensity are alternately exposed singly and in combination to give an intensity step of 2 and therefore a log intensity step of 0.301. These are mounted just above the instrument's optical entrance, and may consist of:

          The lamps available before about 1960 were large and of low wattage and low colour temperature, and their intensities were insufficient to allow accurate calibrations at the higher density end of the wedge. Present day designs use small quartz halogen lamps of higher wattage and higher colour temperature and can be used to calibrate the whole wedge. Komhyr (1980b) reports that essentially identical results were obtained in 1977 from the Canadian device, which uses two 350 W lamps with a prism to ensure coincident beams and is water cooled, and a United States device, which uses two 600 W lamps side by side and is air cooled. The intensity incident on the instrument needs to be stable to about 1% over a measurement cycle and this requires a very stable lamp power supply, good electrical contacts at the lamp, and good mechanical stability of the lamp and its mount. The direct heating of the instrument, largely by conduction, can also be a problem for lamps of large power consumption (Walshaw, 1975, p.66).

          To obtain an initial null balance for the halved intensity at the various points along the wedge, a small lamp and diffuser is mounted in front of slit S4, whose intensity, as measured by the instrument detector, is adjusted until it equals the halved intensity transmitted by the chosen part of the wedge and by S3. Slit S1 is shuttered. The intensity of the S4 lamp should be as stable as those in the two-source device.

          The alternative method of producing intensity step changes is by means of neutral density filters of known transmittance placed inside the instrument in the path of one of the spectral beams, usually that through S3. For example, before the two lamp device was developed, neutral density filters of transmittance 0.25 and 0.75 were used to calibrate the whole wedge (Normand and Kay, 1952). Dobson (1957b) described the use of a rhodium plated neutral density filter to calibrate only the optically dense part of the wedge. The filter's transmittance was calibrated against the optically thin part which had been calibrated with the two lamp method.

          Neutral density filters are relatively easy to make and to use. They may be made of evaporated metals on quartz plates, of perforated plates, or of metal gauzes. Their density may be chosen to be small enough to map small scale variations in wedge density, though it should be noted that because of the density averaging of the S3 slit's length of about 1 cm, such variations will be limited to the order of 0.15 in density. The disadvantage of filters is that their transmittance must be independently calibrated to high accuracy and must be specifically checked for spectral transmittance variations, temperature dependences and temporal changes. As with the two lamp devices, they must provide a uniform intensity across the instrument's field of view, to avoid errors associated with the instrument's spectral sensitivity variation across the field of view (see Section 2.3), and for this reason the use of a single variable iris aperture (Sinha and Sanyal, 1965), which is, in effect, a very spatially non-uniform filter, cannot be recommended.

3.3      Data analysis methods

          The measured (ΔR, R) data set is best checked graphically to eliminate bad data and to ensure sufficient coverage, especially where the density gradient varies rapidly or the data are noisy. The data are smoothed and it is upon this smoothed curve that subsequent processing is done. The simplest method of processing is to assume that the local density gradient dD/dR at any value of R is equal to the coarse density gradient ΔD/ΔR centred on R, and then to integrate ΔD/ΔR, which is the inverse function of the (ΔR, R) function, as a function of R. Some extrapolation at the ends of the density range would be required. This method is briefly discussed by Dobson (1957b, p. 107).

          The recommended analysis procedure in Dobson (1957b) and Komhyr (1980b) makes use of the "minor interval" method, an ingenious procedure which is designed to better describe small scale wedge density variations. There appears to be no wholely mathematical description of the method in the literature, and the descriptions of it in the above two references, and in what follows, are in terms of the steps needed to carry it out. The notation used below is the same as that used in the above references.

          The method is illustrated in Figure 3.2. Using the (ΔR, R) data, sequences of major density intervals F (where F equals 0.301 for a two lamp calibration) are formed along the wedge such that the differences between successive starting points in R (and therefore also between successive end points in R) of each sequence define a set of unknown smaller density intervals fi. The sequence starting points in R are chosen to divide the first major interval into five minor intervals of approximately equal size in R. The sum of the fi, i.e., f1 + f2 + f3 + f4 + f5 equals F. With some thought, it may be seen that the sequences formed repeat the minor density intervals along the wedge. The values of fi are estimated from the R values noted as the sequences are formed, by assuming that the local density gradient is equal to the coarse density gradient over the major R interval in which it is centred. If there are n major density intervals along the wedge, it is possible to make n-l individual estimates of each fi, and these are averaged to give the final value of each fi. The fi are then added up and interpolated, in proper sequence, to give the density at any point along the wedge.

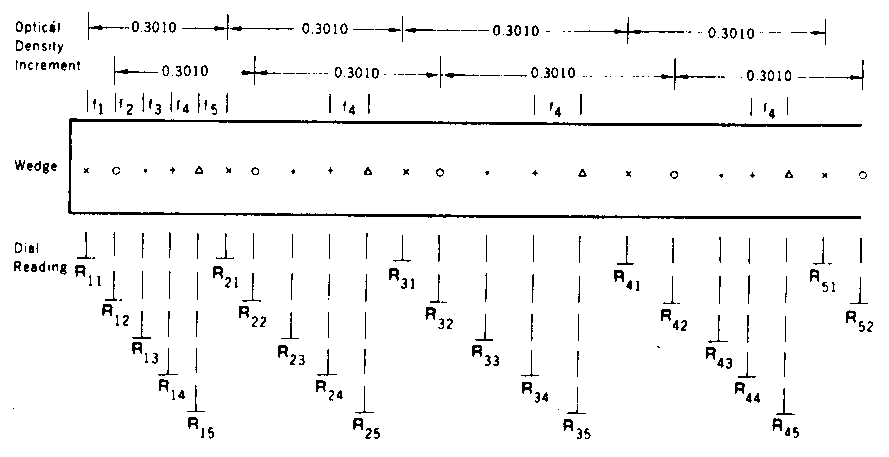
Figure 3.2 
Figure 3.2   Illustration of minor interval method of analysing the Dobson 
             optical wedge calibration data (from Komhyr, 1980b).

          The minor interval method is not easy to understand from such a brief description, and for further details the reader should consult Dobson (1957b) and Komhyr (1980b). It can be noted that the only significant advantage of the minor interval method, compared to the simple integration, is its averaging of up to ten estimates of the fi, and the tendency for this to reduce any systematic error in the estimation of the local gradient from the surrounding coarse gradient. The question as to whether the application of the minor interval method is really necessary can only be answered by an inspection of the density function of the wedge under consideration.

3.4      Error analysis of standard methods

          Let it be assumed, firstly, that there are random uncertainties of 0.1° in the dial readings, secondly, that any systematic measurement uncertainties in dial readings, such as due to operator bias, tend to cancel for differences in dial readings, and thirdly, that a suitable criterion of performance is for the uncertainty in XA total ozone at an airmass of 1 to be less than 0.0015 atm cm (about 0.5%). This criterion implies a wedge density uncertainty of less than 0.0026 at a density of about 0.65, or equivalently 0.4% in density. The corresponding density uncertainties for the C and D bandpairs are 0.35% and 0.25% respectively.

          The random uncertainty for a dial reading difference, ΔR, is thus assumed to be 0.14°. (This may be a conservative value, since the scatter in ΔR in Figure 3.1 appears to be about 0.07°.) This results in an uncertainty of about 2.4% in individual fi estimates for minor intervals of approximately 6° in R, which is in reasonable agreement with the uncertainty apparent in the experimental data of Table 14.3 in Dobson (1957b). If a large number of data contribute to the ( R, R) function, then the size of the random error will reduce, for example, to 1.2% if there are four data per 6° in R, and if nine minor intervals contribute to the average estimate of fi, then the random error in this average will reduce to 0.4% in density, which, by coincidence, equals the error criterion. The constraint that: 

                                      n
                                      Σ fi = F                                           (3.1)
                                     i=1
within each major interval prevents this uncertainty from accumulating along the wedge.

          To minimise the random uncertainty, it is clear, firstly, that many (ΔR, R) data are needed, say, at least four per 6° in R, and secondly that the minor intervals should be no smaller than necessary. Since the S3 slit's length is equivalent to about 20° in R, it would seem sensible to divide the major interval of approximately 30° into only three minor intervals and not the five usually used.

          In both the simple integration method and the minor interval method, it is assumed that the density gradient at a point is closely equal to the coarse density gradient of the ΔR interval in which it is centred. It is not difficult to derive expressions for the systematic error arising from this assumption as applied to polynomial forms. If the density function over the ΔR interval is linear or quadratic, the error is identically zero, but if it is cubic, the error is c(ΔR)2/4, where c is the coefficient of the polynomial's cubic term. This means that there will be essentially no systematic error in the density estimates made from those parts of the (ΔR, R) function which are constant or linear, and hence that particular weight should be given to the minor interval fi estimates made in these parts.

          The variation among a group of fi estimates will give an indication of the size of any cubic or higher order error components present. Another indication may be found, as follows, by comparison to the error that would arise if the quadratic components of the (ΔR, R) function in Figure 3.1 were neglected, i.e., if the function was represented by a linear function. If the proportional error in ΔD/ΔR is taken as equal to the corresponding proportional error in ΔR, i.e.: 

                              δ(ΔD/ΔR)/(ΔD/ΔR) = δ(ΔR)/ΔR                           (3.2)

then the largest deviation in Figure 3.1 from a mean linear function (a triangular shape of height δ(ΔR) = 0.25° and base length R = 40°), would result in a density error of 0.0017, which is only about two thirds of our error criterion. If quadratic errors are so small, then cubic and higher order errors are likely to be insignificant. Indeed, it would seem that for the wedge shown, the simple integration method would give results little different to those given by the minor interval method. However, it is possible that this wedge is a particularly linear one and that other wedges will show greater nonlinearity.

          It is necessary with the simple integration method to extrapolate the (ΔR, R) function by ΔR/2 at either end of the wedge. Exercises similar to that of the preceeding paragraph show that the errors associated with these extrapolations are very small. In any case, the very low density end does not play an important part in operational measurements, and the errors present when the very high density end is in use will be swamped by other instrument error sources, such as stray light.

          Intercomparisons have shown that the variations with airmass (and therefore with wedge density) of the difference between the XAD ozone measurements made by well calibrated instruments can amount to 0.5% or less. This shows that the wedge calibrations were accurate to at least this level, which is the same as the criterion assumed here.

3.5      Error analysis of filter methods

          The effect on wedge calibrations of the transmittance uncertainty in fixed transmittance neutral density filters is analysed here in terms of the error criterion used above, namely, 0.0026 in wedge density at a density of 0.65. A filter's density D and transmittance T are related by: 

                                  T = 10-D                                               (3.3)

and the proportional uncertainties, d and t in D and T respectively are related by: 


                                 t = Td - 1                                              (3.4)

The transmittance accuracies required to ensure that the criterion of d = 0.004 is met are given below in Table 3.1. The listed product Tt is the actual uncertainty in transmittance. 

                        TABLE 3.1

Transmittance uncertainties for various filter densities.

    D             T               t            Tt
   0.10         0.794          0.0009        0.0007
   0.15         0.708          0.0014        0.0010
   0.20         0.631          0.0019        0.0012
   0.30         0.501          0.0028        0.0014
   0.50         0.316          0.0047        0.0015
   1.00         0.100          0.0094        0.0009
   2.00         0.010          0.0187        0.0002

          Table 3.1 could be used as an aid to choosing filter transmittances. Thus to map small scale density variations directly a filter transmittance of about (80±0.07)% might be chosen, while to provide an approximate halving of intensity a transmittance of about (50±0.14)% would be needed. The accuracy requirements for the filters are similar, so the high transmittance filter may be used without serious disadvantage. The corollary is that if a high transmittance filter is insufficiently accurate on its own, then a similarly calibrated halving filter would not be adequate as its calibration reference.

          The most important lesson from the table is that very high accuracies, of about 0.1%, are required of the filter transmittances. Filters may be independently calibrated with quality laboratory spectrophotometers, but even with very careful work these accuracies will be difficult to obtain. Spectral and temperature dependencies and temporal variations must also be accounted for. Transmittance accuracies are likely to be, in general, no better than 0.5%. For these reasons, independently calibrated filters cannot be recommended for calibrating wedges.

          The standard Dobson rhodium plated filters are satisfactory, however, because they are calibrated against the wedge's optically thin end which has been calibrated by the two lamp method, thus making use of the appropriate wavelength bands and the instrument's intrinsic high accuracy for measurements of relative density. The uncertainty of rhodium filter wedge calibrations is probably no greater than twice that of a full two-source calibration, provided the filters' transmittances and any temperature dependences of them are regularly checked.

3.6      Summary

(i)     Modern evaporated metal wedges are very stable and are relatively linear. The original wedges made of carbon black in gelatin were much less stable and linear.

(ii)    The wedges are best calibrated in situ, and by means of the two-source device, which nowadays usually comprises two cooled quartz halogen lamps. The apparatus measures a coarse density gradient and its design and use are well established.

(iii)   Neutral density filters which are independently calibrated cannot be recommended for calibrating wedges as the transmittance accuracy of about 0.001 (i.e., 0.1%) required of the filters is very difficult to obtain and to maintain. The standard rhodium plated neutral density filters are satisfactory if they are calibrated in the standard way against the optically thin end of the wedge.

(iv)    The "minor interval" method is generally the preferred method for processing the coarse density gradient data, but for a wedge of relatively linear gradient, a simple integration will be sufficient. Minor intervals need be no smaller than 10° in dial angle R.

(v)     To minimise systematic error, the averages of the estimates of the minor densities fi should be weighted in favour of those estimates determined from parts of the density gradient function (or R, R function) which are closely linear.

(vi)    Error analysis shows that, with reasonable care, a two-source calibration can give accuracy of 0.4% in wedge density, which is equivalent to an accuracy of about 0.5% in XA. This is supported by field intercomparisons of Dobson instruments, the results of which strongly suggest that the uncertainty in XAD due to wedge calibration can be less than 0.5%.

(vii)   The accuracy of wedge calibrations for gelatin carbon wedges, and for calibrations not made with the two source device, will be less, perhaps equivalent to about 2% in XAD.

Return to Table of Contents

Forward to Stray Light