This is not the latest CarbonTracker update!
Link to latest.
CarbonTracker Documentation
CT2016 release
CarbonTracker Team
Feb 17, 2017
Contents
1 Introduction1.1 A tool for science, and policy
1.2 A community effort
1.3 Updates
1.4 The role of other atmospheric species in constraining the atmospheric carbon budget
2 Terrestrial biosphere module
2.1 CASA model
2.2 Temporal downscaling
2.2.1 Smooth month-to-month variations
2.3 GFED4.1s and GFED_CMS
2.4 References
3 Fire module
3.1 Global Fire Emissions Database (GFED)
3.2 GFED_CMS: Fluxes from the NASA Carbon Monitoring System
3.3 References
4 Fossil fuel module
4.1 The "Miller" emissions dataset
4.2 The "ODIAC" emissions dataset (ODIAC2016)
4.3 Uncertainties
4.4 References
5 Oceans module
5.1 Air-sea gas exchange
5.2 OIF: the Ocean Inversion Fluxes prior
5.3 pCO2-Clim: Takahashi et al. (2009) climatology prior
5.4 Gas-transfer velocity and ocean surface properties
5.5 Specifics of the inversion methodology related to air-sea CO2 fluxes
5.6 References
6 Atmospheric transport
6.1 TM5 offline tracer transport model
6.2 Convective flux fix
6.3 References
7 Observations
7.1 The CarbonTracker observational network
7.2 Adaptive model-data mismatch
7.3 Statistical performance of CT2016
7.4 References
8 Ensemble data assimilation
8.1 Parameterization of unknowns
8.1.1 Optimization regions
8.1.2 Ensemble size and localization
8.1.3 Dynamical model
8.2 Covariance structure
8.3 Multiple prior models
8.3.1 Posterior uncertainties in CarbonTracker
8.4 References
9 Ecoregions in CarbonTracker
9.1 What are ecoregions?
9.2 Why use ecoregions?
9.3 Ecosystems within TransCom regions
9.4 References
1 Introduction
The goal of the CarbonTracker program is to produce quantitative estimates of atmospheric carbon uptake and release for North America and the rest of the world that are consistent with observed patterns of CO2 in the atmosphere.1.1 A tool for science, and policy
CarbonTracker and the associated long-term monitoring of atmospheric CO2 helps improve our understanding of how carbon uptake and release from land ecosystems and oceans are responding to a changing climate, increasing levels of atmospheric CO2 (higher CO2 may enhance plant growth) and other environmental changes, including human management of land and oceans. The open access to all CarbonTracker results means that anyone can scrutinize our work, suggest improvements, and profit from our efforts. This will accelerate the development of a tool that can monitor, diagnose, and possibly predict the behavior of the global carbon cycle, and the climate that is so intricately connected to it. CarbonTracker can become a policy support tool too. Its ability to accurately quantify natural and anthropogenic emissions and uptake at regional scales is currently limited by a sparse observational network. With enough observations, it will become possible to keep track of regional emissions, including those from fossil fuel use, over long periods of time. This will provide an independent check on emissions accounting, estimates of fossil fuel use based on economic inventories. It can thus provide feedback to policies aimed at limiting greenhouse gas emissions. This independent measure of effectiveness of any policy, provided by the atmosphere itself (where CO2 levels matter most), is the bottom line in any mitigation strategy.1.2 A community effort
CarbonTracker is intended to be a tool for the community and we welcome feedback and collaboration from anyone interested. Our ability to accurately track carbon with more spatial and temporal detail is dependent on our collective ability to make enough measurements and to obtain enough air samples to characterize variability present in the atmosphere. For example, estimates suggest that observations from tall communication towers (taller than 200m) can tell us about carbon uptake and emission over a radius of only several hundred kilometers. The shows how sparse the current network is. One way to join this effort is by contributing measurements. Regular air samples collected from the surface, towers or aircraft are needed. It would also be very fruitful to expand use of continuous measurements like the ones now being made on very tall (more than 200m) communications towers. Another way to join this effort is by volunteering flux estimates from your own work, to be run through CarbonTracker and assessed against atmospheric CO2. Please contact us if you would like to get involved and collaborate with us.1.3 Updates
CarbonTracker is updated about once per year to include new data and model improvements. The updated calculations are produced for the year 2000 through the most recent complete year of observations. Previous versions are available at the CarbonTracker website, and the effect of significant changes to any of the system components is noted. Important revisions of our methods for CT2016 include the following:- Use of "adaptive" model-data mismatch scheme.
- Use of hourly data at continuous measurement sites.
- New land and wildfire priors
1.4 The role of other atmospheric species in constraining the atmospheric carbon budget
Many laboratories making high accuracy CO2 observations also make many other measurements of the same air, typically other greenhouse gases such as methane CH4, nitrous oxide N2O, sulfur hexafluoride SF6, as well as carbon monoxide (CO) and isotopic ratios of CO2 and CH4. These measurements are usually made as mole fractions, for reasons explained here. These trace gases are relevant for climate change and interesting in their own right, but the additional measurements can also help in source identification or process understanding. For this reason a series of halocompounds and hydrocarbons have recently been added to the analysis of a subset of air samples. Several of these species can be useful for monitoring air quality, but they can also help with better source apportionment of the greenhouse gases. In addition, the estimation of the source strengths of a number of pollutants could be greatly improved if we were able to quantify fossil fuel CO2 emissions from air measurements for specified regions. The best tracer for quantifying the component of atmospheric CO2 that has been recently added to an air mass through the burning of fossil fuels is the decrease of the carbon-14 content of CO2. Cosmic rays produce carbon-14, a radioactive form of carbon, in the higher regions of the atmosphere. It is present in the atmosphere and oceans and in all living organisms and their remains, but coal, oil, and natural gas contain no carbon-14 because it has long decayed away. Currently, carbon-14 measurements are made on only a small subset of the air samples because of higher analysis costs. None of these other data and their relationships have been used in this release of CarbonTracker. We expect them to be incorporated gradually at later stages. CarbonTracker is a NOAA contribution to the North American Carbon Program.2 Terrestrial biosphere module
The biospheric component of the terrestrial carbon cycle consists of all the carbon stored in `biomass' around us. This includes trees, shrubs, grasses, carbon within soils, dead wood, and leaf litter. Such reservoirs of carbon can exchange CO2 with the atmosphere. Exchange starts when plants take up CO2 during their growing season through the process called photosynthesis (uptake). Most of this carbon is released back to the atmosphere throughout the year through a process called respiration (release). This includes both the decay of dead wood and litter and the metabolic respiration of living plants. Of course, plants can also return carbon to the atmosphere when they burn, as described in Section 3. Even though the yearly sum of uptake and release of carbon amounts to a relatively small number (a few petagrams (one Pg=1015 g)) of carbon per year, the flow of carbon each way is as large as 120 PgC each year. This is why the net result of these flows needs to be monitored in a system such as ours. It is also the reason we need a good physical description (model) of these flows of carbon. After all, from the atmospheric measurements we can only see the small net sum of the large two-way streams (gross fluxes). Information on what the biospheric fluxes are doing in each season, and in every location on Earth is derived from a specialized biosphere model, and fed into our system as a first guess, to be refined by our assimilation procedure.2.1 CASA model
Two biosphere models currently provide first-guess terrestrial fluxes for CT2016. Both models are versions of the Carnegie-Ames Stanford Approach (CASA) biogeochemical model introduced by Potter et al. (1993). CASA calculates global carbon fluxes using input from weather models to drive biophysical processes, and satellite observed Normalized Difference Vegetation Index (NDVI) to track plant phenology. The models are driven by year-specific weather and satellite observations, and include the effects of fires on photosynthesis and respiration (see van der Werf et al., 2006, and Giglio et al., 2006). Both simulations provide 0.5°×0.5° global fluxes with a monthly time resolution. CASA models provide monthly-mean Net Primary Production (NPP) and heteotrophic respiration (RH) for each terrestrial grid cell being simulated. NPP is the difference in photosynthetic carbon uptake (Gross Primary Production, GPP) and the carbon release by the same plants due to "maintenance respiration", which is also called autotrophic respiration, RA. The carbon uptake represented by NPP and carbon release represented by RH can be differenced to provide Net Ecosystem Exchange (NEE) of CO2. Throughout this discussion, we use the convention that fluxes carry algebraic signs and we adopt the "atmospheric perspective" for those signs. Thus carbon uptake by the terrestrial biosphere is a negative flux to the atmosphere, and release of CO2 back to the atmosphere is a positive flux. This means that we represent all respiration fluxes as positive and GPP as negative, so NEE = NPP + RH. This stands in contrast to convention in the terrestrial carbon community, where all fluxes are generally non-negative.2.2 Temporal downscaling
Use of monthly-mean terrestrial fluxes to simulate atmospheric CO2 is not sufficient to resolve the variability observed at measurement sites. Instead, higher-frequency variations, including the diurnal cycle and effects of passing weather systems must be imposed on the CASA monthly fluxes. Following the logic laid out by Olsen and Randerson (2004), we transform the CASA-supplied monthly-mean NPP and RH fluxes into GPP and total ecosystem respiration, RE = RA + RH. To estimate sub-monthly variations, including diurnal and synoptic variability, the Olsen and Randerson (2004) strategy is to model GPP as a linear function of incoming surface solar radiation and total ecosystem respiration as a function of near-surface temperature. The fundamental assumption needed to apply this scheme is that we can resolve CASA-simulated NPP into GPP and RA. We apply the assumption that GPP is twice NPP, which further implies that RA is the same size as NPP (but of opposite sign):
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
2.2.1 Smooth month-to-month variations
While the scheme outlined above imposes realistic diurnal- and synoptic-scale variations on monthly-mean GPP and RE, it still allows for abrupt changes from one month to the next. For CT2016, we add a further processing step designed to remove such unrealistic step changes. We fit smooth curves to the monthly GPP and RE using the piecewise integral quadratic splines (PIQS) of Rasmussen (1991). These PIQS fits are continuous in the first and second derivatives, and have the property of preserving monthly mean flux. We use a similar scheme to smooth over year-to-year step changes in fossil fuel emissions. The final smoothed GPP is
| (8) |
| (9) |
| (10) |
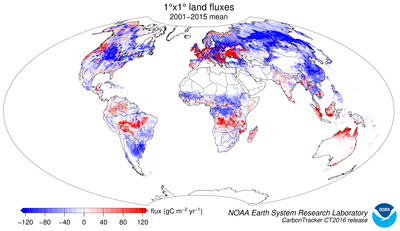
Figure 1: Map of optimized global biosphere fluxes. The pattern of
net ecosystem exchange (NEE) of CO2 of the land biosphere averaged over
the time period indicated, as estimated by CarbonTracker. This NEE
represents land-to-atmosphere carbon exchange from photosynthesis and
respiration in terrestrial ecosystems, and a contribution from fires. It
does not include fossil fuel emissions. Negative fluxes (blue colors)
represent CO2 uptake by the land biosphere, whereas positive fluxes (red
colors) indicate regions in which the land biosphere is a net source of
CO2 to the atmosphere. Units are gC m−2 yr−1.
2.3 GFED4.1s and GFED_CMS
CarbonTracker uses fluxes from CASA runs from two models associated with the GFED project as its first guess for terrestrial biosphere fluxes. We have found a significantly better match to observations when using this output compared to the fluxes from a neutral biosphere simulation. Both of the CASA simulations used in CT2016 (GFED 4.1s and GFED_CMS) are driven by AVHRR NDVI. This satellite driver tends to produce a larger-amplitude annual cycle of NEE compared to the alternative driver, MODIS fPAR. As one of the robust results of atmospheric invrsions is a deeper annual cycle of terrestrial NEE, inversions using NDVI-driven first-guess fluxes perform slightly better than those with a MODIS fPAR driver. The record of atmospheric CO2 calls for a deeper terrestrial biosphere sink than that generally simulated by forward models like CASA. This is manifested by a larger annual cycle of terrestrial biosphere fluxes, and in particular a deeper boreal summer uptake of carbon dioxide, in the posterior optimized fluxes compared to the prior models (See Fig. 2). We call upon the atmospheric CO2 observations to make this change, and in order to handle these prior model differences the ensemble Kalman filter's prior covariance model has been re-tuned. In short, this prior uncertainty needs to comfortably span differences among the terrestrial biosphere priors, the fossil fuel emissions priors, and adjustments to fluxes required to bring model predictions into agreement with observations. As a result, the land biosphere prior uncertainty is larger in CT2016 in comparison to previous releases. Details can be found in Section 8.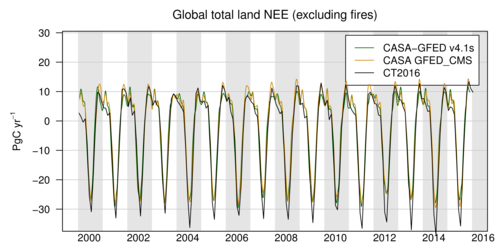
Figure 2: Time series of global-total terrestrial biosphere flux between
the two priors and the CT2016 posterior. Global CO2 uptake by the land
biosphere, expressed in PgC yr−1, excluding emissions by wildfire.
Positive flux represents emission of CO2 to the atmosphere, and the
negative fluxes indicate times when the land biosphere is a sink of CO2.
Optimization against atmospheric CO2 data requires a larger land sink
than in either prior, which effectively requires a deeper annual cycle.
This is shown by the CT2016 posterior (black).
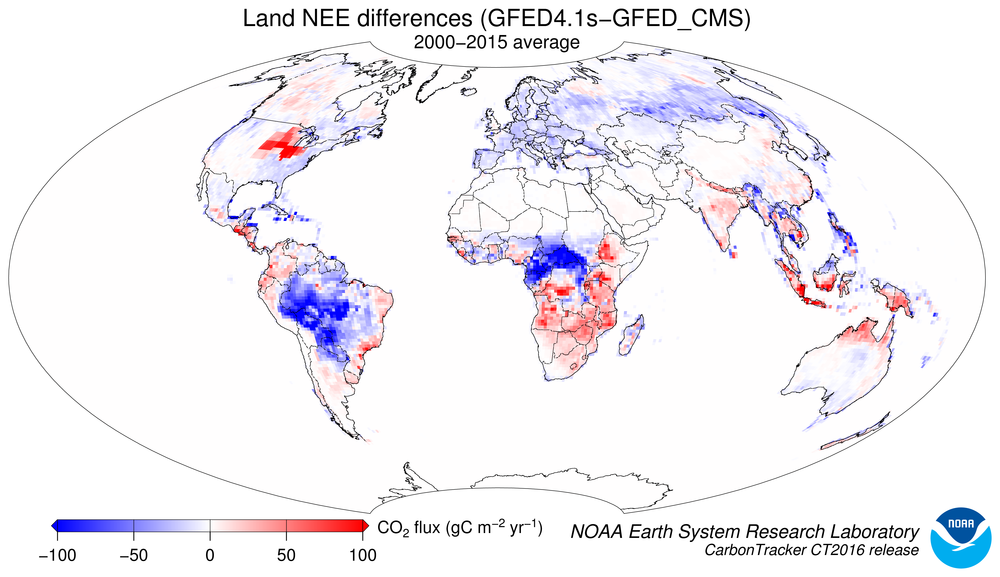
Figure 3: Differences in long-term mean terrestrial biosphere fluxes
between the two priors. Red indicates areas where the GFED4.1s prior has
less terrestrial uptake (or more outgassing to the atmosphere) than the
GFED_CMS prior, and blue represents the opposite. Units are gC m−2 yr−1.
CarbonTracker CT2016 is a full reanalysis of the 2000-2015 period
using new fossil fuel emissions, CASA-GFED v4.1s and GFED_CMS fire
emissions, and first-guess biosphere model fluxes derived from
CASA-GFED v4.1s for 4 of our inversions, and from CASA GFED_CMS for
the remaining 4 inversions.
Due to the inclusion of fires, inter-annual variability in weather and
NDVI, the fluxes for North America start with a small net
flux even when no assimilation is done. This first-guess flux ranges
from neutral exchange to about 0.5 PgC yr−1 of uptake.
2.4 References
- Potter, C. S., J. T. Randerson, C. B. Field, P. A. Matson, P. M. Vitousek, H. A. Mooney, and S. A. Klooster (1993), Terrestrial ecosystem production: A process model based on global satellite and surface data, Global Biogeochem. Cycles, 7(4), 811–841, doi:10.1029/93GB02725.
- van der Werf, G. R., Randerson, J. T., Collatz, G. J. and Giglio, L. (2003), Carbon emissions from fires in tropical and subtropical ecosystems. Global Change Biology, 9: 547–562. doi:10.1046/j.1365-2486.2003.00604.x
- Jim Randerson research group
- Global Fire Emissions Database (GFED) web page
- Olsen, S. C., and J. T. Randerson (2004), Differences between surface and column atmospheric CO2 and implications for carbon cycle research, J. Geophys. Res., 109, D02301, doi:10.1029/2003JD003968.
- Giglio, L., van der Werf, G. R., Randerson, J. T., Collatz, G. J., and Kasibhatla, P.: Global estimation of burned area using MODIS active fire observations, Atmos. Chem. Phys., 6, 957-974, doi:10.5194/acp-6-957-2006, 2006.
- van der Werf, G. R., Randerson, J. T., Giglio, L., Collatz, G. J., Kasibhatla, P. S., and Arellano Jr., A. F.: Interannual variability in global biomass burning emissions from 1997 to 2004, Atmos. Chem. Phys., 6, 3423-3441, doi:10.5194/acp-6-3423-2006, 2006.
- L.A Rasmussen, Piecewise integral splines of low degree, Computers & Geosciences, Volume 17, Issue 9, 1991, Pages 1255-1263, ISSN 0098-3004, http://dx.doi.org/10.1016/0098-3004(91)90027-B.
- NASA GFED_CMS CASA project
3 Fire module
Vegetation fires are an important part of the carbon cycle and have been so for many millennia. Even before human civilization began to use fires to clear land for agricultural purposes, most ecosystems were subject to natural wildfires that would rejuvenate old forests and bring important minerals to the soils. When fires consume part of the landscape in either controlled or natural burning, carbon dioxide (amongst many other gases and aerosols) is released in large quantities. Each year, vegetation fires emit around 2 PgC as CO2 into the atmosphere, mostly in the tropics. Currently, a large fraction of wildfire is started by humans. This is mostly intentional to clear land for agriculture, or to re-fertilize soils before a new growing season. This important component of the carbon cycle is monitored mostly from space, while sophisticated `biomass burning' models are used to estimate the amount of CO2 emitted by each fire. Such estimates are then used in CarbonTracker to prescribe the emissions. These emissions are not modified in the optimization (inverse modeling) process. In CT2016 we use two fire emissions datasets, each with at least daily temporal resolution. The GFED4.1s emissions are modeled at 3-hourly intervals, and GFED_CMS emissions are available at daily resolution.3.1 Global Fire Emissions Database (GFED)
CT2016 uses GFED4.1s as one of the fire modules to estimate biomass burning. GFED4.1s is a variant of the CASA biogeochemical model as described in the terrestrial biosphere model documentation to estimate the carbon fuel in various biomass pools. The dataset consists of 1° × 1° gridded monthly burned area, fuel loads, combustion completeness, and fire emissions (Carbon, CO2, CO, CH4, NMHC, H2, NOx, N2O, PM2.5, Total Particulate Matter, Total Carbon, Organic Carbon, Black Carbon) for the time period spanning January 1997 - December 2015, of which we currently only use CO2. The GFED burned area is based on MODIS satellite observations of fire counts. These, together with detailed vegetation cover information and a set of vegetation specific scaling factors, allow predictions of burned area over the time span that active fire counts from MODIS are available. The relationship between fire counts and burned area is derived, for the specific vegetation types, from a `calibration' subset of 500m resolution burned area from MODIS in the period 2001-2004. Once burned area has been estimated globally, emissions of trace gases are calculated using the CASA biosphere model. The seasonally changing vegetation and soil biomass stocks in the CASA model are combusted based on the burned area estimate, and converted to atmospheric trace gases using estimates of fuel loads, combustion completeness, and burning efficiency. For CT2016, we also apply temporal scaling factors updated from Mu et al. (2011) to downscale the GFED4.1s CO2 emissions from monthly averages to emissions with 3-hourly resolution.3.2 GFED_CMS: Fluxes from the NASA Carbon Monitoring System
The NASA GFED_CMS team uses a variant of the GFED4 system to produce alternative fire emissions. This model uses GIMSS NDVI, the GFEDv3 fire model and GFEDv4 burned area. Fire emissions are available on a daily basis from 2003-2015. For 2000-2002, we apply the climatology of GFED_CMS fire emissions, computed from its 2003-2015 mean. Note that the GFED_CMS team produces temporally-downscaled GPP, heterotrophic respiration, and fires with 3-hourly resolution. This is done using MERRA meteorology using a scheme similar to Olsen and Randerson (2004). We do not use this downscaled product, in part because the MERRA meteorology is different from the ECMWF meteorology, and in part because the spatial resolution of the MERRA meteorology is different from our 1° × 1° flux grid. This means that we are limited to daily resolution of GFED_CMS fire emissions: unlike the GFED4.1s fire emissions, these have no diurnal cycle.3.3 References
- Giglio, L., J. T. Randerson, and G. R. van der Werf, (2013), Analysis of daily, monthly, and annual burned area using the fourth-generation global fire emissions database (GFED4) J. Geophys. Res. Biogeosci., 118, 317–328, doi:10.1002/jgrg.20042.
- van der Werf, G. R., Randerson, J. T., Collatz, G. J. and Giglio, L. (2003), Carbon emissions from fires in tropical and subtropical ecosystems. Global Change Biology, 9: 547–562. doi:10.1046/j.1365-2486.2003.00604.x
- van der Werf, G. R., Randerson, J. T., Giglio, L., Collatz, G. J., Mu, M., Kasibhatla, P. S., Morton, D. C., DeFries, R. S., Jin, Y., and van Leeuwen, T. T.: Global fire emissions and the contribution of deforestation, savanna, forest, agricultural, and peat fires (1997–2009), Atmos. Chem. Phys., 10, 11707-11735, doi:10.5194/acp-10-11707-2010, 2010.
- Akagi, S. K., Yokelson, R. J., Wiedinmyer, C., Alvarado, M. J., Reid, J. S., Karl, T., Crounse, J. D., and Wennberg, P. O.: Emission factors for open and domestic biomass burning for use in atmospheric models, Atmos. Chem. Phys., 11, 4039-4072, doi:10.5194/acp-11-4039-2011, 2011.
- Mu, M., Randerson, J. T., van der Werf, G. R., Giglio, L., Kasibhatla, P., Morton, D., Collatz G. J., DeFries, R. S., Hyer, E. J., Prins, E. M., Griffith, D. W. T., Wunch, D., Toon, G. C., Sherlock, V., and Wennberg, P. O. (2011), Daily and 3-hourly variability in global fire emissions and consequences for atmospheric model predictions of carbon monoxide, J. Geophys. Res., 116, D24303, doi:10.1029/2011JD016245.
- Andreae, M. O., and P. Merlet (2001), Emission of trace gases and aerosols from biomass burning, Global Biogeochem. Cycles, 15(4), 955–966, doi:10.1029/2000GB001382.
- Giglio, L., van der Werf, G. R., Randerson, J. T., Collatz, G. J., and Kasibhatla, P.: Global estimation of burned area using MODIS active fire observations, Atmos. Chem. Phys., 6, 957-974, doi:10.5194/acp-6-957-2006, 2006.
- van der Werf, G. R., Randerson, J. T., Giglio, L., Collatz, G. J., Kasibhatla, P. S., and Arellano Jr., A. F.: Interannual variability in global biomass burning emissions from 1997 to 2004, Atmos. Chem. Phys., 6, 3423-3441, doi:10.5194/acp-6-3423-2006, 2006.
- Jim Randerson research group
- Global Fire Emissions Database (GFED) web page
- GFED_CMS web page at NACP
4 Fossil fuel module
Human beings first influenced the carbon cycle through land-use change. Early humans used fire to control animals and later cleared forests for agriculture. Over the last two centuries, following the industrial and technical revolutions and continuing global population increase, fossil fuel combustion has become the largest anthropogenic source of CO2. In 2013, fossil fuel combustion was responsible for nearly 10 billion metric tons of carbon emitted to the atmosphere. Coal, oil and natural gas combustion are the most common energy sources in both developed and developing countries. Important sectors of the economy-power generation, transportation, residential & commercial building heating, and industrial processes-rely on fossil fuel combustion. According to the Carbon Dioxide Information and Analysis Center (CDIAC), world emissions of CO2 from fossil fuel burning, cement manufacturing, and flaring reached 9.8 PgC yr−1 (one PgC=1015 grams of carbon) in 2013 (Boden et al., 2016). Estimates extrapolated by the CarbonTracker team indicate that global total emissions remained nearly steady between 2013 and 2015.. Despite this apparent stabilization, 2014 & 2015 emissions are 59% larger than those in 1990. U.S. input of CO2 to the atmosphere from fossil fuel burning in 2015 was 1.4 PgC, representing 14% of the global total. North American emissions have remained nearly constant since 2000, with a slight decrease in recent years. On the other hand, emissions from developing economies such as the People's Republic of China have been increasing. Emissions from China in 2015 were 2.6 PgC yr−1, representing 27% of the global total. After the economic slowdown which affected many countries starting in 2008, fossil fuel emissions have rebounded, and in many parts of the world continue to increase. The U.S. Department of Energy's International Energy Outlook 2013 projects that the global total source will reach 12.4 PgC yr−1 in 2040. This may be an underestimate, however, as that same report projects 2020 emissions of 9.9 PgC yr−1, a figure that was nearly reached in 2014. In nearly all global and regional carbon flux estimation systems, including CarbonTracker, fossil fuel CO2 emissions are not optimized. Instead, these emissions are imposed and are not subject to revision by the estimation framework. Global mass balance requires that any errors in fossil fuel emissions be compensated by opposing errors in land and ocean CO2 exchange. Thus it is vital that fossil fuel CO2 emissions are prescribed accurately, so that flux estimates for the land biosphere and oceans are robust. The fossil fuel emissions source data we use are available on an annually-integrated global and national basis. This aggregate information needs to be gridded before being incorporated into CarbonTracker. The major uncertainty in this process is distributing the national-annual emissions spatially across a nation and temporally into monthly contributions. In CT2016, two different fossil fuel CO2 emissions datasets were used to help assess the uncertainty in this mapping process. These two emissions products are called the "Miller" and "ODIAC" emissions datasets. These two datasets have very similar global and national emissions for each year, but differ in how those emissions are distributed spatially and temporally. Whereas previous CarbonTracker releases used monthly-constant fossil fuel emissions, in CT2015 we introduced the use of temporal scaling factors to simulate day-of-week and diurnal variability for those emissions. These "Temporal Improvements for Modeling Emissions by Scaling" (TIMES) scaling factors, introduced by Nassar et al. (2013), are again applied to both the Miller and ODIAC emissions modules for CT2016. The scaling factors consist of seven day-of-week global scaling factor maps, and 24 hourly global scaling factor maps to represent the diurnal cycle. For use in TM5, the hourly scaling factors were aggregated to three-hourly factors to accommodate the time step of the model.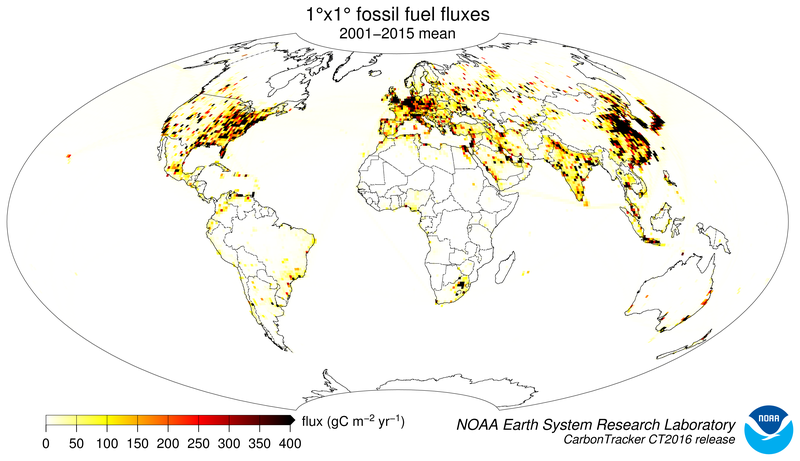
Figure 4: Spatial distribution of fossil fuel emissions. This
is a spatial average of the Miller and ODIAC emissions inventories.
4.1 The "Miller" emissions dataset
- Global Totals The Miller fossil fuel emission inventory is derived from independent global total and spatially-resolved inventories. Annual global total fossil fuel CO2 emissions are from the Carbon Dioxide Information and Analysis Center (CDIAC, Boden et al.2013) which extend through 2010. In order to extrapolate these fluxes through 2015, we extrapolate using the percentage increase or decrease for each fuel type (solid, liquid, and gas) in each country from the 2016 BP Statistical Review of World Energy for 2011-2015. To estimate emissions for the first two months of 2016 (required by CarbonTracker's 5-week assimilation window), no increase is applied to 2015 values.
- Spatial Distribution Miller fossil-fuel CO2 fluxes are spatially distributed in two steps: First, the coarse-scale country totals through 2010 (from Boden et al. 2013) are mapped onto a 1° × 1° grid according to the spatial patterns from the EDGAR v4.2 inventories (European Commission, 2009). The spatial pattern varies by year up until the end of the EDGAR v4.2 product in 2008. After this, the trends estimated in each pixel are linearly extrapolated. Note that while EDGAR provides annual emissions estimates at 1° × 1° resolution, their totals do not agree with those from CDIAC. Thus, only the spatial patterns in EDGAR are used. The CDIAC country-by-country totals sum to about 95% of the global total emissions; the remaining 5% is mapped to global shipping routes according to EDGAR, which we treat as a proxy for bunker fuel emissions.
- Temporal Distribution For North America between 30 and 60°N, the Miller system imposes a seasonal cycle derived from the first and second harmonics (Thoning et al., 1989) of the Blasing et al. (2005) analysis for the United States. The Blasing analysis has 10% higher emissions in winter than in summer. This scheme defines a fixed fraction of emissions for each month, so while the shape of the annual cycle is invariant, the amplitude of that cycle scales with the annual total emissions. For Eurasia, a set of seasonal emissions factors from EDGAR distributed by emissions sector is used to define fossil fuel seasonality. As in North America, this seasonality is imposed only from 30-60°N. The Eurasian seasonal amplitude is about 25%, significantly larger than that in North America, owing to the absence of a secondary summertime maximum due to air conditioning. See Figure 5 for the resulting time series of fossil fuel emissions. In order to avoid discontinuities in the fossil fuel emissions between consecutive years, a spline curve that conserves annual totals (Rasmussen 1991) is fit to seasonal emissions in each 1° × 1° grid cell.
4.2 The "ODIAC" emissions dataset (ODIAC2016)
- Global Totals The ODIAC fossil fuel emission inventory (Oda and Maksyutov, 2011) is also derived from independent global and country emission estimates from CDIAC, but national emission estimates used were taken from the year 2016 edition of CDIAC estimates (Boden et al.2016). Annual country total fossil fuel CO2 emissions from CDIAC which extend through 2013, were extrapolated through 2015 using the BP Statistical Review of World Energy. Difference between the CDIAC global total and country-by-country totals were ascribed to the entire emissions field. The same adjustment was done for the year extrapolated using using the CDIAC global total (2000-2015).
- Spatial Distribution ODIAC emissions are spatially distributed using many available "proxy data" that explain spatial extent of emissions according to emission types (emissions over land, gas flaring, aviation and marine bunker). Emissions over land were distributed in two steps: First, emissions attributable to power plants were mapped using geographical locations (latitude and longitude) provided by the global power plant dataset CARbon Monitoring and Action, CARMA. Next, the remaining land emissions (i.e. land total minus power plant emissions) were distributed using nightlight imagery collected by U.S. Air Force Defense Meteorological Satellite Project (DMSP) satellites. Emissions from gas flaring were also mapped using nightlight imagery. Emissions from aviation were mapped using flight tracks adopted from UK AERO2k air emission inventory. It should be noted that currently, air traffic emissions are emitted at ground level within CarbonTracker. Emissions from marine bunker fuels are placed entirely in the ocean basins along shipping routes according to patterns from the EDGAR database.
- Temporal Distribution The CDIAC estimates used for mapping emissions in ODIAC only describe how much CO2 was emitted in a given year. To present seasonal changes in emissions, we used the CDIAC 1° × 1° monthly fossil fuel emission inventory (Andres et al. 2011). The CDIAC monthly data utilizes the top 20 emitting countries' fuel (coal, oil and gas) consumption statistics available to estimate seasonal change in emissions. Monthly emission numbers at each pixel were divided by annual total and then a fraction to annual total was obtained. Monthly emissions in the ODIAC inventory were derived by multiplying this fraction by the emission in each grid cell.
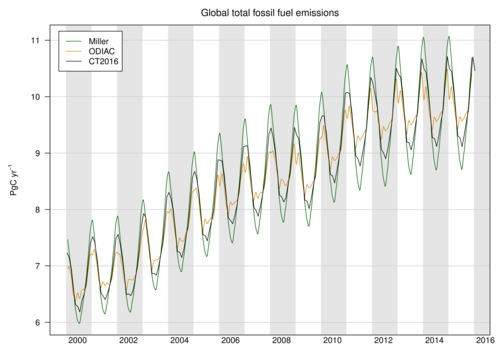
Figure 5: Time series of global fossil fuel emissions. The Miller (green)
and ODIAC (tan) estimates are each used by half of the sixteen inversions
in the CT2016 suite, so the CT2016 (black) inventory is effectively an
average of Miller and ODIAC. Note that fossil fuel emissions are not
optimized in CarbonTracker.
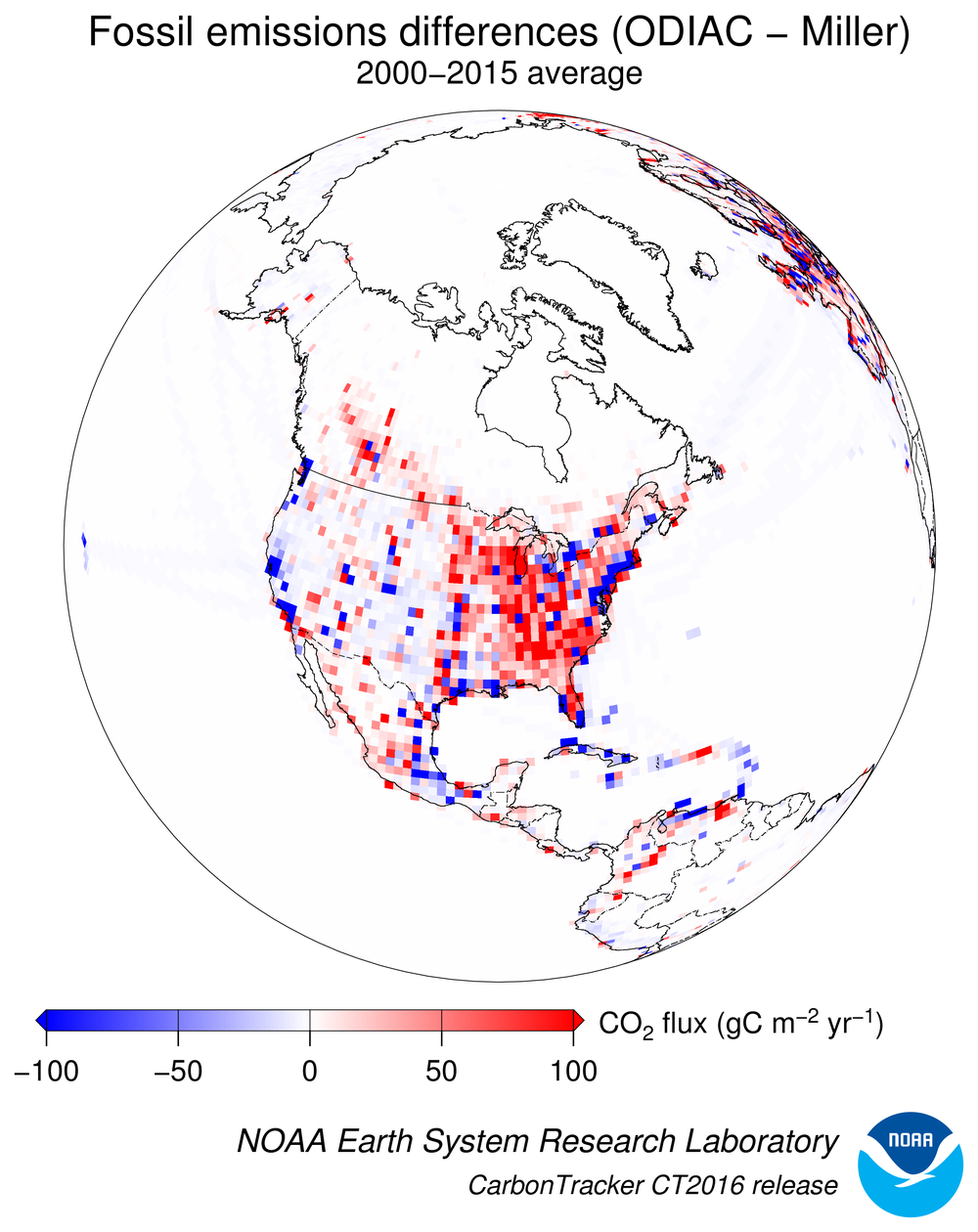
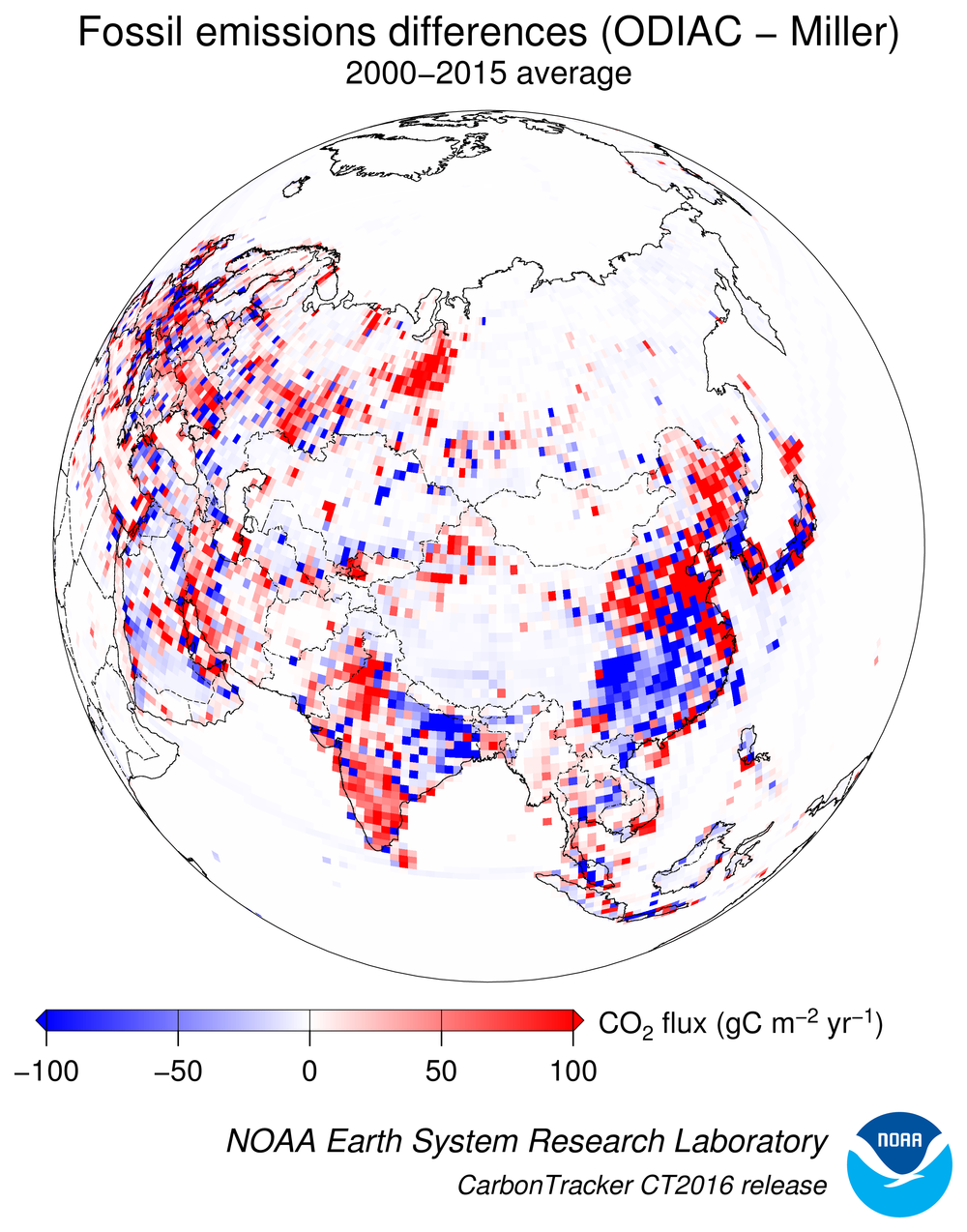
Figure 6: Spatial differences in long-term mean fossil fuel emissions
between the two priors. Note that both the Miller and ODIAC emissions
inventories use the same country totals, but have different models for
spatial distribution of that flux within countries.
4.3 Uncertainties
Marland (2008) attached an uncertainty of about 5% (95% confidence interval; approximately 2-σ) to the global total fossil fuel source. Recent estimates by Andres et al. (2014) put a larger uncertainty of 8.4% (2-σ) on the CDIAC global total. Uncertainties for individual regions of the world, and for sub-annual time periods are likely to be larger. Additional uncertainties are introduced when the emissions are distributed in space and time. In the Miller dataset, the overall Eurasian seasonality is based on scaling factors derived only from Western Europe and thus highly uncertain, but most likely a better representation than assuming no emission seasonality at all. Similarly, the use of the CDIAC monthly emission dataset for modeling seasonality introduces additional uncertainty in ODIAC. The additional uncertainty for the global total in the monthly CDIAC emission, which is solely due to the method for estimating seasonality, is reported as 6.4% (Andres et al. 2011). As mentioned earlier, fossil fuel emissions are not optimized in the current CarbonTracker system, similar to nearly all carbon data analysis systems. Spatial and temporal atmospheric CO2 gradients arise from terrestrial biosphere and fossil-fuel sources. These gradients, which are interpreted by CarbonTracker, are difficult to attribute to one or the other cause. This is because atmospheric sampling sites have historically been established in locations remote from biospheric and anthropogenic sources, especially in the temperate Northern Hemisphere. Given that surface CO2 flux due to biospheric activity and oceanic exchange is much more uncertain compared to fossil fuel emissions, CarbonTracker, like most current carbon dioxide data assimilation systems, does not attempt to optimize fossil fuel emissions. That is, the contribution of CO2 from fossil fuel burning to observed CO2 mole fractions is considered known. As detailed above, however, in CarbonTracker an effort is made to account for some aspects of fossil fuel uncertainty by using two different fossil fuel estimates. From a technical point of view, extra land biosphere prior flux uncertainty is included in the system to represent the random errors in fossil fuel emissions. Eventually, fossil fuel emissions could be optimized within CarbonTracker, especially with the addition of 14CO2 observations as constraints (Basu et al. 2016).4.4 References
- Nassar, R., L. Napier-Linton, K. R. Gurney, R. J. Andres, T. Oda, F. R. Vogel, and F. Deng (2013), Improving the temporal and spatial distribution of CO2 emissions from global fossil fuel emission data sets, J. Geophys. Res. Atmos., 118, 917–933, doi:10.1029/2012JD018196.
- CDIAC Annual Global and National fluxes
- DOE Energy Information Administration (EIA)
- BP Statistical Review of World Energy
- EDGAR Database
- CDIAC (Blasing et al.) Monthly USA fluxes
- L.A Rasmussen, Piecewise integral splines of low degree, Computers & Geosciences, Volume 17, Issue 9, 1991, Pages 1255-1263, ISSN 0098-3004, http://dx.doi.org/10.1016/0098-3004(91)90027-B.
- Thoning, K. W., P. P. Tans, and W. D. Komhyr (1989), Atmospheric carbon dioxide at Mauna Loa Observatory: 2. Analysis of the NOAA GMCC data, 1974–1985, J. Geophys. Res., 94(D6), 8549–8565, doi:10.1029/JD094iD06p08549.
- Marland, G. (2008), Uncertainties in Accounting for CO2 from Fossil Fuels, Journal of Industrial Ecology, 12(2), 136-139.
- Boden, T.A., G. Marland, and R.J. Andres. 2016. Global, Regional, and National Fossil-Fuel CO2 Emissions. Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge, Tenn., U.S.A. DOI: 10.3334/CDIAC/00001_V2016
- CDIAC Preliminary 2011 and 2012 Global and National Estimates)
- The Center for Global Development, CARbon Monitoring Action (CARMA) power plant database
- DMSP satellite nightlight data
- Centre for Air Transport and the Environment (CATE), AERO2k aviation emissions inventory
- Andres, R. J., J. S. Gregg, L. Losey, G. Marland, T. A. Boden (2011) Monthly, global emissions of carbon dioxide from fossil fuel consumption. Tellus B, 63:309-327. doi: 10.1111/j.1600-0889.2011.00530.x.
- Andres R.J., T.A. Boden, G. Marland, Monthly Fossil-Fuel CO2 Emissions: Mass of Emissions Gridded by One Degree Latitude by One Degree Longitude, doi:10.3334/CDIAC/ffe.MonthlyMass.2015
- Oda, T. and Maksyutov, S.: A very high-resolution (1 km × 1 km) global fossil fuel CO2 emission inventory derived using a point source database and satellite observations of nighttime lights, Atmos. Chem. Phys., 11, 543-556, doi:10.5194/acp-11-543-2011, 2011.
- European Commission, Joint Research Centre (JRC)/Netherlands Environmental Assessment Agency (PBL). (2009) Emission Database for Global Atmospheric Research (EDGAR), release version 4.0
- Andres, Robert J.; Boden, Thomas A.; Higdon, David (2014). A new evaluation of the uncertainty associated with CDIAC estimates of fossil fuel carbon dioxide emission. Tellus B, 66, doi:10.3402/tellusb.v66.23616
- S. Basu, J. B. Miller, and S. Lehman. Separation of biospheric and fossil fuel fluxes of CO2 by atmospheric inversion of CO2 and 14CO2 measurements: Observation system simulations. Atmos. Chem. Phys, 16(9):5665–5683, 2016.
5 Oceans module
The oceans play an important role in the Earth's carbon cycle. They are the largest long-term sink for carbon and have an enormous capacity to store and redistribute CO2 within the Earth system. Oceanographers estimate that about 48% of the CO2 from fossil fuel burning has been absorbed by the ocean (Sabine et al., 2004). The dissolution of CO2 in seawater shifts the balance of the ocean carbonate equilibrium towards a more acidic state with a lower pH. This effect is already measurable (Caldeira and Wickett, 2003), and is expected to become an acute challenge to shell-forming organisms over the coming decades and centuries. Although the oceans as a whole have been a relatively steady net carbon sink, CO2 can also be released from oceans depending on local temperatures, biological activity, wind speeds, and ocean circulation. These processes are all considered in CarbonTracker, since they can have significant effects on the ocean sink. Improved estimates of the air-sea exchange of carbon in turn help us to understand variability of both the atmospheric burden of CO2 and terrestrial carbon exchange.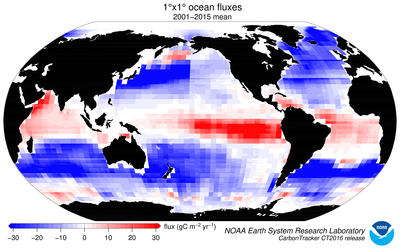
Figure 7: Posterior long-term mean ocean fluxes from
CarbonTracker. The pattern of air-sea exchange of CO2 averaged over the
time period indicated, as estimated by CarbonTracker. Negative fluxes
(blue colors) represent CO2 uptake by the ocean, whereas positive fluxes
(red colors) indicate regions in which the ocean is a net source of CO2
to the atmosphere. Units are gC m−2 yr−1.
The initial release of CarbonTracker (CT2007) used climatogical estimates
of CO2 partial pressure in surface waters (pCO2) from Takahashi et al.
(2002) to compute a first-guess air-sea flux. This air-sea pCO2
disequilibrium was modulated by a surface barometric pressure correction
before being multiplied by a gas-transfer coefficient to yield a flux.
Starting with CT2007B and continuing through the CT2011_oi
release, the air-sea pCO2 disequilibrium was imposed from analysis of
ocean inversions ("OIF", cf. Jacobson et al., 2007) results, with
short-term flux variability derived from the atmospheric model wind
speeds via the gas transfer coefficient. The barometric pressure
correction was removed so that climatological high- and low-pressure
cells did not bias the long-term means of the first guess fluxes.
In CT2016, two models are used to provide prior estimates of air-sea
CO2 flux. The OIF scheme provides one of these flux priors, and
the other is an updated version of the Takahashi et al. pCO2
climatology.
5.1 Air-sea gas exchange
Oceanic uptake of CO2 in CarbonTracker is computed using air-sea differences in partial pressure of CO2 inferred either from ocean inversions (called "OIF" henceforth), or from a compilation of direct measurements of seawater pCO2 (called "pCO2-clim" henceforth). These air-sea partial pressure differences are combined with a gas transfer velocity computed from wind speeds in the atmospheric transport model to compute fluxes of carbon dioxide across the sea surface. In either method, the first-guess fluxes have no interannual variability (IAV) other than a smooth trend. IAV in oceanic CO2 flux is due to anomalies in surface pCO2, such as those that occur in the tropical eastern Pacific during an El Niño, and to associated variability in winds, ocean circulation, and sea-surface properties. In CarbonTracker, only the surface winds (and hence gas transfer), manifest these interannual anomalies; the remaining IAV of flux must be inferred from atmospheric CO2 signals. In the following sections we describe the two ocean flux prior models. We then describe the air-sea gas transfer velocity parameterization and discuss detais of the inversion methodology specific to oceanic exchange of CO2.5.2 OIF: the Ocean Inversion Fluxes prior
For the OIF prior, long-term mean air-sea fluxes and the uncertainties associated with them are derived from the ocean interior inversions reported in Jacobson et al. (2007). These ocean inversion flux estimates are composed of separate preindustrial (natural) and anthropogenic flux inversions based on the methods described in Gloor et al. (2003) and biogeochemical interpretations of Gruber, Sarmiento, and Stocker (1996). The uptake of anthropogenic CO2 by the ocean is assumed to increase in proportion to atmospheric CO2 levels, consistent with estimates from ocean carbon models. OIF contemporary pCO2 fields were computed by summing the preindustrial and anthropogenic flux components from inversions using five different configurations of the Princeton/GFDL MOM3 ocean general circulation model (Pacanowski and Gnanadesikan, 1998), then dividing by a gas transfer velocity computed from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA40 reanalysis. There are two small differences in first-guess fluxes in this computation from those reported in Jacobson et al. (2007). First, the five OIF estimates all used Takahashi et al. (2002) pCO2 estimates to provide high-resolution patterning of flux within inversion regions (the alternative "forward" model patterns were not used). To good approximation, this choice only affects the spatial and temporal distribution of flux within each of the 30 ocean inversion regions, not the magnitude of the estimated flux. Second, wind speed differences between the ERA40 product used in the offline analysis and the ECMWF operational model used in the online CarbonTracker analysis result in small deviations from the OIF estimates. Other than the smooth trend in anthropogenic flux assumed by the OIF results, interannual variability (IAV) in the first guess ocean flux comes entirely from wind speed effects on the gas transfer velocity. This is because the ocean inversions retrieve only a long-term mean and smooth trend.5.3 pCO2-Clim: Takahashi et al. (2009) climatology prior
The pCO2-Clim prior is derived from the Takahashi et al. (2009) climatology of seawater pCO2. This climatology was created from about 3 million direct observations of seawater pCO2 around the world between 1970 and 2007. With the exception of measurements in the Bering Sea, these observations were all linearly extrapolated to the corresponding month of the year 2000 by assuming a constant trend of 1.5 μatm yr−1. This set of global monthly measurements corrected to the reference year 2000 was then interpolated onto a regular grid using a modeled surface current field. The Takahashi et al. (2009) product goes beyond providing this estimate of surface water pCO2. They also compute climatological air-sea exchange of CO2 by using the GLOBALVIEW-CO2 atmospheric carbon dioxide product to compute air-sea ∆pCO2, sea surface properties inferred from ocean climatologies, and winds from atmospheric reanalysis to estimate gas-transfer velocity. Unlike many other atmospheric analyses, we have chosen not to use the climatological fluxes as our prior, nor to use the climatological ∆pCO2. Instead, we take only the seawater pCO2 distribution from the Takahashi et al. climatology-our atmospheric model provides both pCO2 in the air at the sea surface and the winds needed to estimate gas transfer. Seawater pCO2 is extrapolated from 2000 to the actual year of the CarbonTracker simulation using a presumed increase of 1.5 μatm yr−1 at every point in the global ocean. This is the same trend used in Takahashi et al. to normalize observations from many years to the reference year of the analysis (2000).5.4 Gas-transfer velocity and ocean surface properties
Both priors use CO2 solubilities and Schmidt numbers computed from World Ocean Atlas 2009 (WOA09) climatological fields of sea surface temperature (Locarnini et al., 2010) and sea surface salinity (Antonov et al., 2010) fields. Gas transfer velocity in CarbonTracker is parameterized as a quadratic function of wind speed following Wanninkhof (1992), using the formulation for instantaneous winds. Gas exchange is computed every 3 hours using wind speeds from the ECMWF operational model as represented by the atmospheric transport model. Air-sea transfer is inhibited by the presence of sea ice, and for this work fluxes are scaled by the daily sea ice fraction in each gridbox provided by the ECMWF forecast data.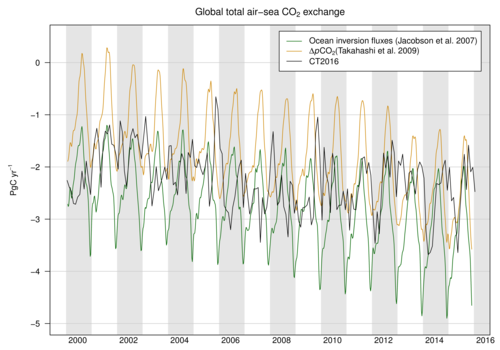
Figure 8: Comparison of air-sea flux priors and the CT2016
posterior. Global CO2 uptake by the ocean, expressed in
PgC yr−1. Positive flux represents a gain of CO2 to the
atmosphere, and the negative numbers here indicate that the ocean is
a sink of CO2. While both priors manifest similar trends of
increasing oceanic uptake of CO2, the OIF prior (in green) has
more oceanic uptake and a greater annual cycle than the
pCO2-clim prior (in tan). The CT2016 across-model posterior
estimate is shown in black for comparison.
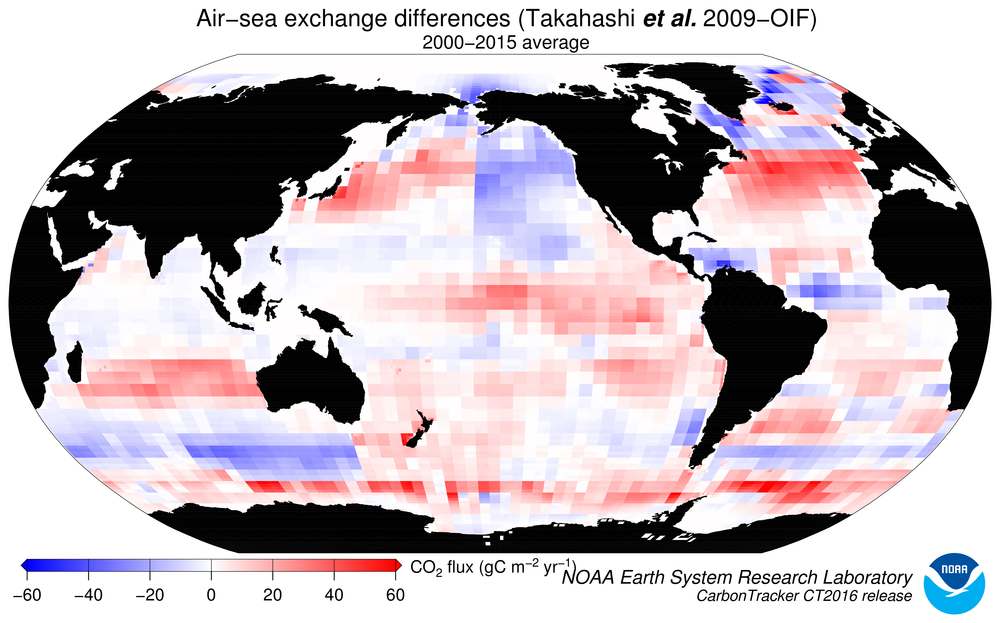
Figure 9: Differences in long-term mean ocean fluxes between the two
priors. Red indicates areas where the pCO2-clim prior has less oceanic
uptake (or more outgassing to the atmosphere) than the OIF prior, and
blue represents the opposite. Units are gC m-2 yr-1.
5.5 Specifics of the inversion methodology related to air-sea CO2 fluxes
The first-guess fluxes described here are subject to scaling during the CarbonTracker optimization process, in which atmospheric CO2 mole fraction observations are combined with transport simulated by the atmospheric model to infer flux signals. Prior air-sea fluxes are adjusted within each of of the 30 ocean inversion regions. In this process, signals of terrestrial flux in atmospheric CO2 distribution can be erroneously interpreted as being caused by oceanic fluxes. This flux "aliasing" or "leakage" is evident in some regions as a change in the shape of the seasonal cycle of air-sea flux. Prior uncertainties for the OIF and pCO2-clim models are specified as uncertainties on scaling factors multiplying net CO2 flux in each of the 30 ocean inversion regions. The pCO2-clim prior has independent regional uncertainties (a diagonal prior covariance matrix), with the uncertainty standard deviation on each region set to 40%. The OIF prior uncertainty has a fully-covariate covariance matrix with off-diagonal elements representing the results of the ocean inversion of Jacobson et al. (2007). The pre-industrial flux uncertainty is time-independent, but the anthropogenic flux uncertainty grows in time as anthropogenic flux uptake increases. The latter is scaled to the simulation date, then added to the former. Total uncertainties are consistent with the Jacobson et al. (2007) results.5.6 References
- NOAA Pacific Marine Environmental Laboratory
- Ocean Acidification
- Locarnini, R. A., A. V. Mishonov, J. I. Antonov, T. P. Boyer, H. E. Garcia, O. K. Baranova, M. M. Zweng, and D. R. Johnson, 2010. World Ocean Atlas 2009, Volume 1: Temperature. S. Levitus, Ed. NOAA Atlas NESDIS 68, U.S. Government Printing Office, Washington, D.C., 184 pp.
- Antonov, J. I., D. Seidov, T. P. Boyer, R. A. Locarnini, A. V. Mishonov, H. E. Garcia, O. K. Baranova, M. M. Zweng, and D. R. Johnson, 2010. World Ocean Atlas 2009, Volume 2: Salinity. S. Levitus, Ed. NOAA Atlas NESDIS 69, U.S. Government Printing Office, Washington, D.C., 184 pp.
- Caldeira, K., and M. E. Wickett (2003), Anthropogenic carbon and ocean pH, Nature, 425365-365, doi:10.1038/425365a
- GLOBALVIEW-CO2 Cooperative Atmospheric Data Integration Project - Carbon Dioxide. CD-ROM, NOAA ESRL, Boulder, Colorado (Also available on Internet via anonymous FTP to ftp.cmdl.noaa.gov, Path: ccg/co2/GLOBALVIEW), 2011.
- Gloor, M., N. Gruber, J. Sarmiento, C. L. Sabine, R. A. Feely, and C. Rödenbeck (2003), A first estimate of present and preindustrial air-sea CO2 flux patterns based on ocean interior carbon measurements and models, Geophysical Research Letters, 30, doi: 10.1029/2002GL015594.
- Gruber, N., J. L. Sarmiento, and T. F. Stocker (1996), An improved method for detecting anthropogenic CO2 in the oceans, Global Biogeochem. Cycles, 10(4), 809–837, doi:10.1029/96GB01608.
- Jacobson, A. R., S. E. Mikaloff Fletcher, N. Gruber, J. L. Sarmiento, and M. Gloor (2007), A joint atmosphere-ocean inversion for surface fluxes of carbon dioxide: 1. Methods and global-scale fluxes, Global Biogeochem. Cycles, 21, GB1019, doi:10.1029/2005GB002556.
- Ronald C. Pacanowski and Anand Gnanadesikan, 1998: Transient Response in a Z-Level Ocean Model That Resolves Topography with Partial Cells. Mon. Wea. Rev., 126, 3248–3270. doi: http://dx.doi.org/10.1175/1520-0493(1998)126<3248:TRIAZL>2.0.CO;2
- Sabine, C. L., R. A. Feely, N. Gruber, R. M. Key, K. Lee, J. L. Bullister, R. Wanninkhof, C. S. Wong, D. W. R. Wallace, B. Tilbrook, F. J. Millero, T. H. Peng, A. Kozyr, T. Ono, and A. F. Rios (2004), The oceanic sink for anthropogenic CO2, Science, 305, 367-371, DOI: 10.1126/science.1097403
- Taro Takahashi, Stewart C. Sutherland, Colm Sweeney, Alain Poisson, Nicolas Metzl, Bronte Tilbrook, Nicolas Bates, Rik Wanninkhof, Richard A. Feely, Christopher Sabine, Jon Olafsson, Yukihiro Nojiri, Global sea–air CO2 flux based on climatological surface ocean pCO2, and seasonal biological and temperature effects, Deep Sea Research Part II: Topical Studies in Oceanography, Volume 49, Issues 9–10, 2002, Pages 1601-1622, ISSN 0967-0645, http://dx.doi.org/10.1016/S0967-0645(02)00003-6.
- Taro Takahashi, Stewart C. Sutherland, Rik Wanninkhof, Colm Sweeney, Richard A. Feely, David W. Chipman, Burke Hales, Gernot Friederich, Francisco Chavez, Christopher Sabine, Andrew Watson, Dorothee C.E. Bakker, Ute Schuster, Nicolas Metzl, Hisayuki Yoshikawa-Inoue, Masao Ishii, Takashi Midorikawa, Yukihiro Nojiri, Arne Körtzinger, Tobias Steinhoff, Mario Hoppema, Jon Olafsson, Thorarinn S. Arnarson, Bronte Tilbrook, Truls Johannessen, Are Olsen, Richard Bellerby, C.S. Wong, Bruno Delille, N.R. Bates, Hein J.W. de Baar, Climatological mean and decadal change in surface ocean pCO2, and net sea-–air CO2 flux over the global oceans, Deep Sea Research Part II: Topical Studies in Oceanography, Volume 56, Issues 8–10, April 2009, Pages 554-577, ISSN 0967-0645, http://dx.doi.org/10.1016/j.dsr2.2008.12.009.
- Wanninkhof, R. (1992), Relationship between wind speed and gas exchange over the ocean, J. Geophys. Res., 97(C5), 7373–7382, doi:10.1029/92JC00188.
6 Atmospheric transport
The link between observations of CO2 in the atmosphere and the exchange of CO2 at the Earth's surface is transport in the atmosphere: storm systems, cloud complexes, and weather of all sorts cause winds that transport CO2 around the world. As a result, local surface CO2 exchange events like fires, forest growth, and ocean upwelling can have impacts at remote locations. To simulate the winds and the weather, CarbonTracker uses sophisticated numerical models that are driven by the daily weather forecasts from the specialized meteorological centers of the world. Since CO2 does not decay or react in the lower atmosphere, the influence of emissions and uptake in locations such as North America and Europe are ultimately seen in our measurements even at the South Pole. Getting the transport of CO2 just right is an enormous challenge, and costs us almost all of the computer resources for CarbonTracker. To represent the atmospheric transport, we use the Transport Model 5 (TM5). This is a community-supported model whose development is shared among many scientific groups with different areas of expertise. TM5 is used for many applications other than CarbonTracker, including forecasting air-quality, studying the dispersion of aerosols in the tropics, tracking biomass burning plumes, and predicting pollution levels that future generations might have to deal with.6.1 TM5 offline tracer transport model
TM5 is an offline global chemical transport model with two-way nested grids. In this global model, regions for which high-resolution simulations are desired can be nested in the coarser global grid. The advantage to this approach is that transport simulations can be performed with a regional focus without the need for boundary conditions. Further, this approach allows measurements outside the "zoom" domain to constrain regional fluxes in the data assimilation, and ensures that regional estimates are consistent with global constraints. TM5 is based on a predecessor model TM3, with improvements in the advection scheme, vertical diffusion parameterization, and meteorological preprocessing of the wind fields (Krol et al., 2005). The model is developed and maintained jointly by the Institute for Marine and Atmospheric Research Utrecht (IMAU, The Netherlands), the Joint Research Centre (JRC, Italy), the Royal Netherlands Meteorological Institute (KNMI), the Netherlands Institude for Space Research (SRON), and the NOAA Earth System Research Laboratory (ESRL). In CarbonTracker, TM5 separately simulates advection, deep and shallow convection, and vertical diffusion in both the planetary boundary layer and free troposphere. The carbon dioxide concentrations predicted by CarbonTracker do not feed back onto these predictions of winds. Prior to use in TM5, ECMWF meteorological data are preprocessed into coarser grids, with attention to retrieving a flow that conserves tracer mass. Like most numerical weather prediction models, advection in the parent ECMWF model is not strictly mass-conserving, so this step is crucial. In CarbonTracker, TM5 is currently run at a global 3° longitude × 2° latitude resolution with a nested regional grid over North America at 1° × 1° resolution (Figure 10). TM5 uses a dynamically-variable time step with a maximum length of 90 minutes. This overall timestep is dynamically reduced to maintain numerical stability, generally during times of high wind speeds. The timestep is divided in half and individual advection, diffusion, convection, and chemistry operators are applied symmetrically in each half step. Furthermore, transport operators in nested grids are modeled at shorter timesteps, so processes at the finest scales are conducted at an effective timestep of one-quarter the overall timestep. See Krol et al. (2005) for details.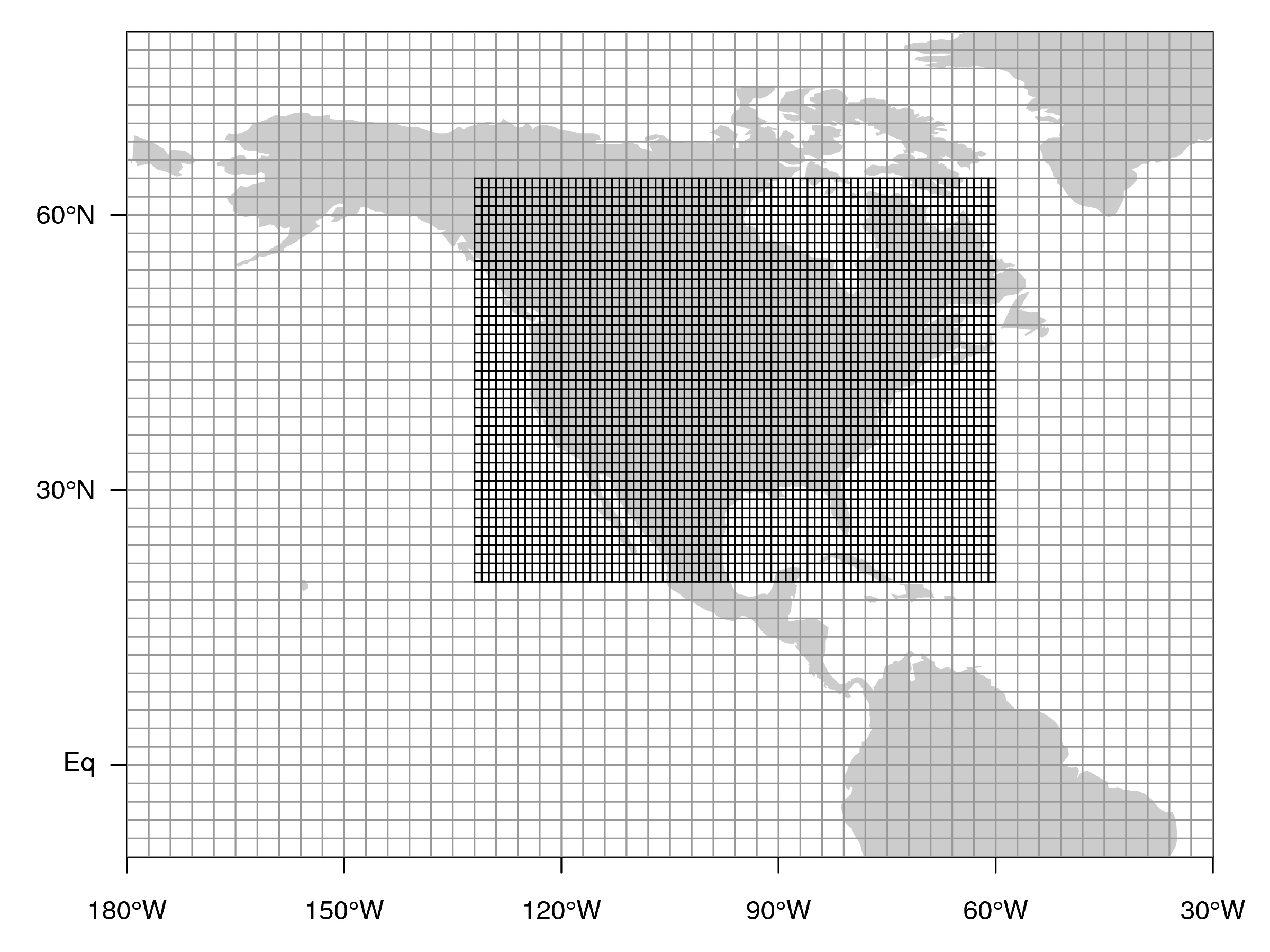
Figure 10: Nested grids used in CarbonTracker over North America. TM5 is
a global model, but it employs nested grids to provide higher
resolution over regions of interest. This figure shows the
1° × 1° nested regional grid over North America and a portion of
the global 3° longitude × 2° latitude grid.
The winds which drive TM5 come from the ERA-interim reanalysis
implemented in the European Centre for
Medium-Range Weather Forecasts (ECMWF) modeling system. The
ERA-Interim reanalysis uses Cy31r2 version of the ECMWF Integrated
Forecast System (IFS) model, which was used for the operational
forecasts up until June 2007. That model uses a 30-minute time step
and a a spectral T255 horizontal resolution, which corresponds to
approximately 79 km spacing on a reduced Gaussian grid. This version
of the IFS has 60 model layers in the vertical, of which TM5 uses a
25-layer subset. These levels are listed in Table 1.
| Model Level | Mean Height (m) | Model Level | Mean Height (m) |
| 1 | 25 | 14 | 9114 |
| 2 | 103 | 15 | 10588 |
| 3 | 247 | 16 | 12184 |
| 4 | 480 | 17 | 13928 |
| 5 | 814 | 18 | 15843 |
| 6 | 1259 | 19 | 17983 |
| 7 | 1822 | 20 | 20412 |
| 8 | 2508 | 21 | 24433 |
| 9 | 3317 | 22 | 30003 |
| 10 | 4248 | 23 | 35895 |
| 11 | 5300 | 24 | 43210 |
| 12 | 6467 | 25 | 123622 |
| 13 | 7741 |
Table 1: Mean mid-level heights above ground in meters for the TM5
model using ERA-interim transport.
6.2 Convective flux fix
Until recently, TM5 was known to have difficulties representing the global surface distribution of sulfur hexafluoride (SF6, see Figure 11 and Peters et al., 2004). SF6 is a nearly inert tracer in the atmosphere, with very small surface and atmospheric sinks and an atmospheric lifetime of about 1,000 years. Consequently, its global budget is very well known from observations alone. It is thought to be released mainly via leakage from electrical transformers. Since the electrical distribution system is closely tied to fossil fuel consumption, SF6 is often considered an analog for fossil fuel CO2 in the atmosphere. It is useful for understanding the rate at which Northern Hemisphere land surfaces are ventilated to the free troposphere, and the rate of interhemispheric exchange in models (Patra et al., 2011). As a result of more than a decade's worth of work on understanding the apparently sluggish mixing in TM5 as revealed by SF6 simulations, a fault in one of the vertical mixing parameterizations of the model was discovered. When it was originally created, TM5 implemented the same planetary boundary layer (PBL) mixing and convection schemes as the parent ECMWF model. Recent comparisons between TM5, the ECMWF parent model, and radiosonde profile data show that the PBL scheme in TM5 performs similarly to that of the parent ECMWF model. The convective scheme, however, does not produce similar results in TM5 as compared to the ECMWF model.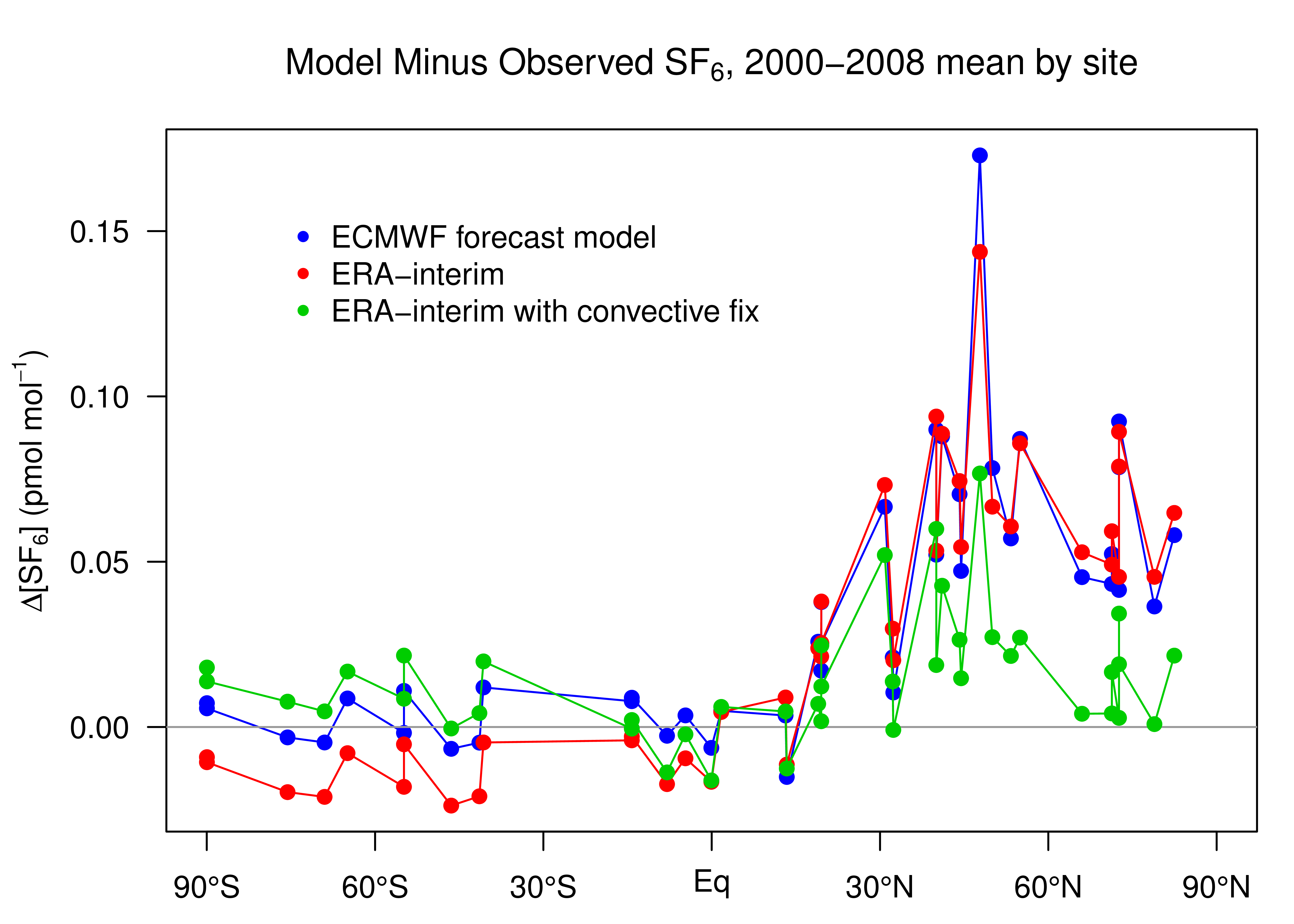
Figure 11: Long-term mean model residuals of SF6 concentrations
as a function of latitude. Residuals are defined as
model-minus-observation, so a positive residual indicates the model
has too much SF6. Three different transport model
simulations are shown. The ECMWF forecast (blue) and ERA-interim
(red) transport simulations do not include the recent "convective
flux fix". The ERA-interim with this convective flux fix is shown
in green. Units are pmol mol−1, or parts per trillion. CT2016 uses
the ERA-interim transport with the convective flux
fix.
In a previous configuration of TM5, the convective entrainment and
detrainment mass fluxes of the parent ECMWF model were re-diagnosed
within TM5 using other meteorological information. The ECMWF model is
used to produce both operational forecasts and the ERA-interim
reanalysis, but the convective fluxes are stored for the ERA-interim
product only. Thus, using ERA-interim meteorology, a direct
comparison is possible. This comparison revealed that the TM5
internal rediagnosis of convective fluxes was faulty. TM5 was
subsequently modified to use parent model ERA-interim convective
fluxes directly. Using the parent model convective fluxes result in a
significantly better SF6 simulations. Simulations with these
parent-model convective fluxes are said to use the "convective flux
fix". Simulations with the convective flux fix show significantly
improved agreement with SF6 observations (see Figure
11).
Since the parent-model convective fluxes are only available for the
ERA-interim product, CT2016 uses only ERA-interim transport with the
convective flux fix. Previous releases of CarbonTracker also used the
ECMWF operational model transport, for which parent-model convective
fluxes are not available. We believe that TM5 simulations without the
parent-model convective fluxes are faulty and should not be included
in our product. When the convective flux fix was instituted in
CT2013B, it resulted in the largest realignment of surface CO2
fluxes in the history of the CarbonTracker program. This is a
prominent example of the sensitive reliance of atmospheric inversions
on accurate atmospheric transport.
6.3 References
- Krol, M., Houweling, S., Bregman, B., van den Broek, M., Segers, A., van Velthoven, P., Peters, W., Dentener, F., and Bergamaschi, P.: The two-way nested global chemistry-transport zoom model TM5: algorithm and applications, Atmos. Chem. Phys., 5, 417-432, doi:10.5194/acp-5-417-2005, 2005.
- Krol, M., Houweling, S., Bregman, B., van den Broek, M., Segers, A., van Velthoven, P., Peters, W., Dentener, F., and Bergamaschi, P.: The two-way nested global chemistry-transport zoom model TM5: algorithm and applications, Atmos. Chem. Phys., 5, 417-432, doi:10.5194/acp-5-417-2005, 2005.
- Denning, A. S., Holzer, Mark., Gurney, K. R., Heimann, M., Law, R. M., Rayner, P. J., Fung, I. Y., Fan, S.-M., Taguchi, S., Friedlingstein, P., Balkanski, Y., Taylor, J., Maiss, M. and Levin, I. (1999), Three-dimensional transport and concentration of SF6. Tellus B, 51: 266–297. doi: 10.1034/j.1600-0889.1999.00012.x
- Patra, P. K., Houweling, S., Krol, M., Bousquet, P., Belikov, D., Bergmann, D., Bian, H., Cameron-Smith, P., Chipperfield, M. P., Corbin, K., Fortems-Cheiney, A., Fraser, A., Gloor, E., Hess, P., Ito, A., Kawa, S. R., Law, R. M., Loh, Z., Maksyutov, S., Meng, L., Palmer, P. I., Prinn, R. G., Rigby, M., Saito, R., and Wilson, C.: TransCom model simulations of CH4 and related species: linking transport, surface flux and chemical loss with CH4 variability in the troposphere and lower stratosphere, Atmos. Chem. Phys., 11, 12813-12837, doi:10.5194/acp-11-12813-2011, 2011.
- Peters, W., M. C. Krol, E. J. Dlugokencky, F. J. Dentener, P. Bergamaschi, G. Dutton, P. v. Velthoven, J. B. Miller, L. Bruhwiler, and P. P. Tans (2004), Toward regional-scale modeling using the two-way nested global model TM5: Characterization of transport using SF6, J. Geophys. Res., 109, D19314, doi:10.1029/2004JD005020
7 Observations
The observations of atmospheric CO2 mole fraction made by NOAA ESRL and partner laboratories are at the heart of CarbonTracker. They inform us on changes in the carbon cycle, whether those changes are regular (such as the annual cycle of growth and decay of leaves and other plant matter), or irregular (such as the release of tons of carbon by a wildfire). The results in CarbonTracker depend directly on the quality, location, and frequency of avaiable observations. The level of detail at which we can retrieve information on the carbon cycle increases strongly with the density of the CO2 observing network.7.1 The CarbonTracker observational network
Observations simulated by CT2016 are suppplied by the GLOBALVIEW+ data product, available at the NOAA ESRL ObsPack web site. This study uses measurements of air samples collected at 136 sites around the world by 32 laboratories:- Commonwealth Scientific and Industrial Research Organization, Oceans & Atmosphere Flagship - GASLAB (CSIRO)
- Instituto de Pesquisas Energeticas e Nucleares (IPEN)
- Environment and Climate Change Canada (ECCC)
- Finnish Meteorological Institute (FMI)
- Laboratoire des Sciences du Climat et de l'Environnement - UMR8212 CEA-CNRS-UVSQ (LSCE)
- University of Heidelberg, Institut für Umweltphysik (UHEI-IUP)
- Umweltbundesamt, Station Schauinsland (UBA-SCHAU)
- Hungarian Meteorological Service (HMS)
- Center for Atmospheric and Oceanic Studies, Tohoku University (TU)
- Meteorological Research Institute (MRI)
- Japan Meteorological Agency (JMA)
- National Institute for Environmental Studies (NIES)
- Comprehensive Observation Network for TRace gases by AirLiner (CONTRAIL)
- University of Groningen (RUG), Centre for Isotope Research (CIO) (RUG)
- Energy Research Centre of the Netherlands (ECN)
- National Institute of Water and Atmospheric Research (NIWA)
- University of Science and Technology (AGH)
- South African Weather Service (SAWS)
- Izana Atmospheric Research Center, Meteorological State Agency of Spain (AEMET)
- Swiss Federal Laboratories for Materials Science and Technology (EMPA)
- World Meteorological Organization/Global Atmosphere Watch (WMO/GAW)
- University of Bern, Physics Institute, Climate and Environmental Physics (KUP)
- University of East Anglia (UEA)
- NOAA Global Monitoring Division (NOAA)
- National Center For Atmospheric Research (NCAR
- Scripps Institution of Oceanography (SIO)
- Harvard University (HU)
- Lawrence Berkeley National Laboratory and ARM Climate Research Facility (LBNL-ARM)
- HIAPER Pole-to-Pole Observations project (HIPPO)
- University of Wisconsin (UOFWI)
- Savannah River National Laboratory (SRNL)
- Lawrence Berkeley National Laboratory (LBNL)
- The source assimilation data: the GLOBALVIEWplus v2.1 (2016) ObsPack
- Simulated values of the source assimilation data: the CT2016 ObsPack
- "Prepped" source assimilation data, reformatting the source GLOBALVIEW 2.1 ObsPack into daily netCDF files containing observations from all datasets, and adding assimilation constraints: the prepped model inputs ObsPack
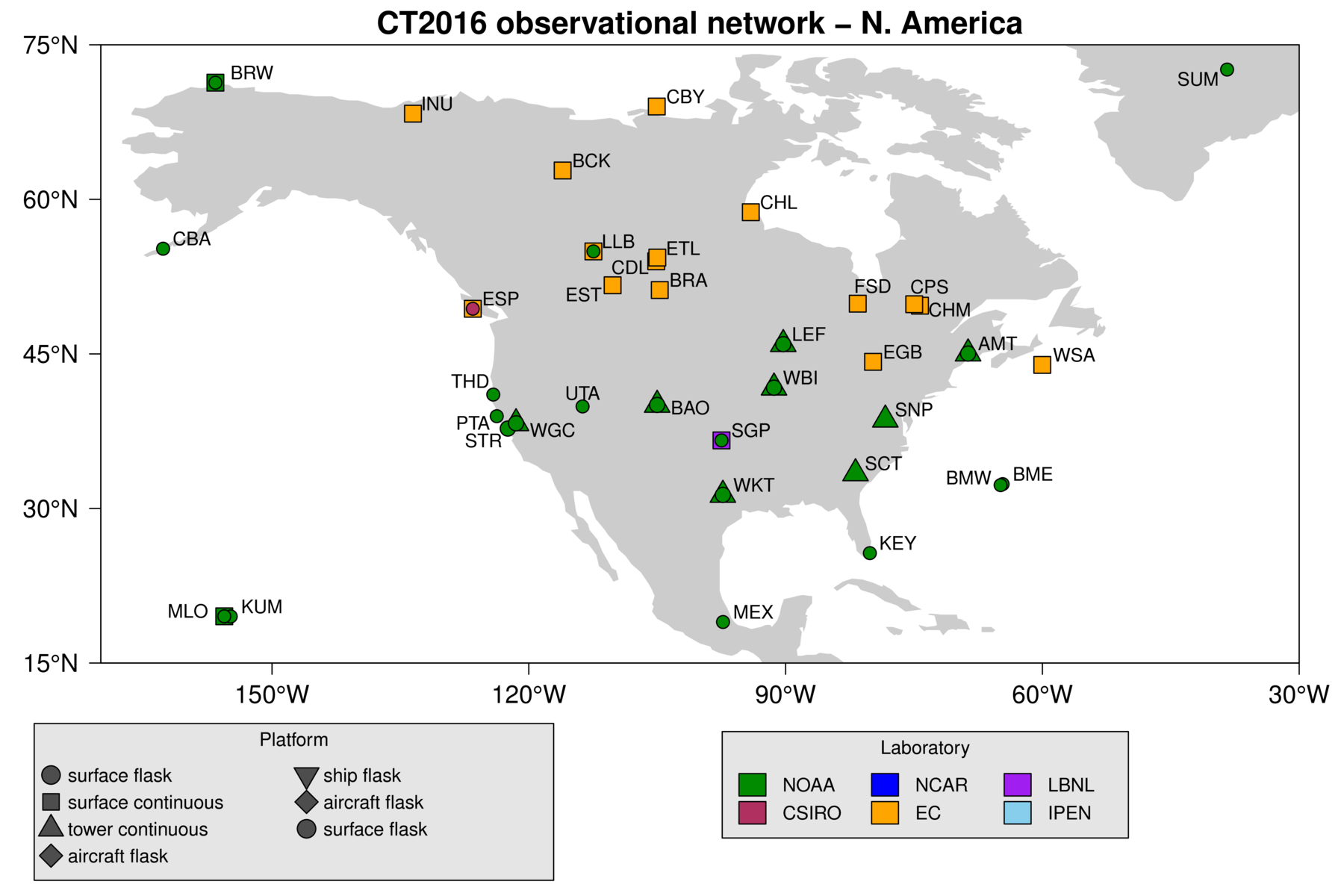
Figure 12: CarbonTracker observational network over North America. See
the CarbonTracker
interactive
network map for more details.
With the advent in 2015 of GLOBALVIEW+, data are now
presented to CarbonTracker with a higher temporal frequency than in
past observational products. At sites with quasi-continuous
monitoring, CT2016 now assimilates hourly average CO2
concentrations. In the past, a single daily assimilation value was
constructed at these sites, generally a four-hour average during
well-mixed background conditions. At continental sites, this
four-hour period was generally from local noon to 4pm; at many
mountain sites background conditions are met at nighttime when upslope
winds are rare. With GLOBALVIEW+, CarbonTracker now
assimilates each hourly average during these background conditions
independently.
Note that all of these observations are calibrated against the same
world CO2 standard (WMO-X2007).
At most quasi-continuous sampling sites, we assimilate only local
afternoon mole fraction observations, recognizing that our atmospheric
transport model does not always capture the stable planetary boundary
layer over land. Daytime well-mixed conditions are much easier to
match using global, coarse-resolution transport models of this class.
Starting with GLOBALVIEW+, we generally use the recommendations of
data providers as to which observations are appropriate for
assimilation. Such observations are identified by a variable in the
ObsPack distribution, obs_flag. Only observations with obs_flag = 1
are identified for assimilation by data providers. We modify the
designation of assimilation data for Environment and Climate Change
Canada quasi-continuous sampling sites. For these data, obs_flag is
set to 1 by the data provider for times when they represent the daily
minimum CO2 concentration. This is generally later in the day
than our standard scheme of local noon-4pm used to represent times of
well-mixed PBLs. For these datasets, we have changed obs_flag to
indicate assimilation only for the local noon - 4pm time period.
These selected observations are further filtered based on the CCG
curve fitting routine of Thoning et al.(1989). This filter fits a
smooth curve to the selected observations, and measurements more than
3 standard deviations away from this curve are excluded from
assimilation.
At mountain-top sites (e.g. MLO, NWR, and SPL), it is usually
nighttime hours that are selected for assimilation, as these tend to
be the most stable time period. Nighttime hours also avoid periods of
upslope flows that contain local vegetative and/or anthropogenic
influence.
Data from the Sutro tower (STR_01P0) and the Boulder tower (BAO_01P0,
BAO_01C3) are strongly influenced by local urban emissions, which
CarbonTracker is unable to resolve. At these two sites, pollution events
have been identified using co-located measurements of carbon monoxide.
In this study, measurements thought to be affected by pollution events
have been excluded. This technique is under active refinement.
Note that aircraft observations are not assimilated, but are
instead retained for independent cross-validation of CarbonTracker
results.
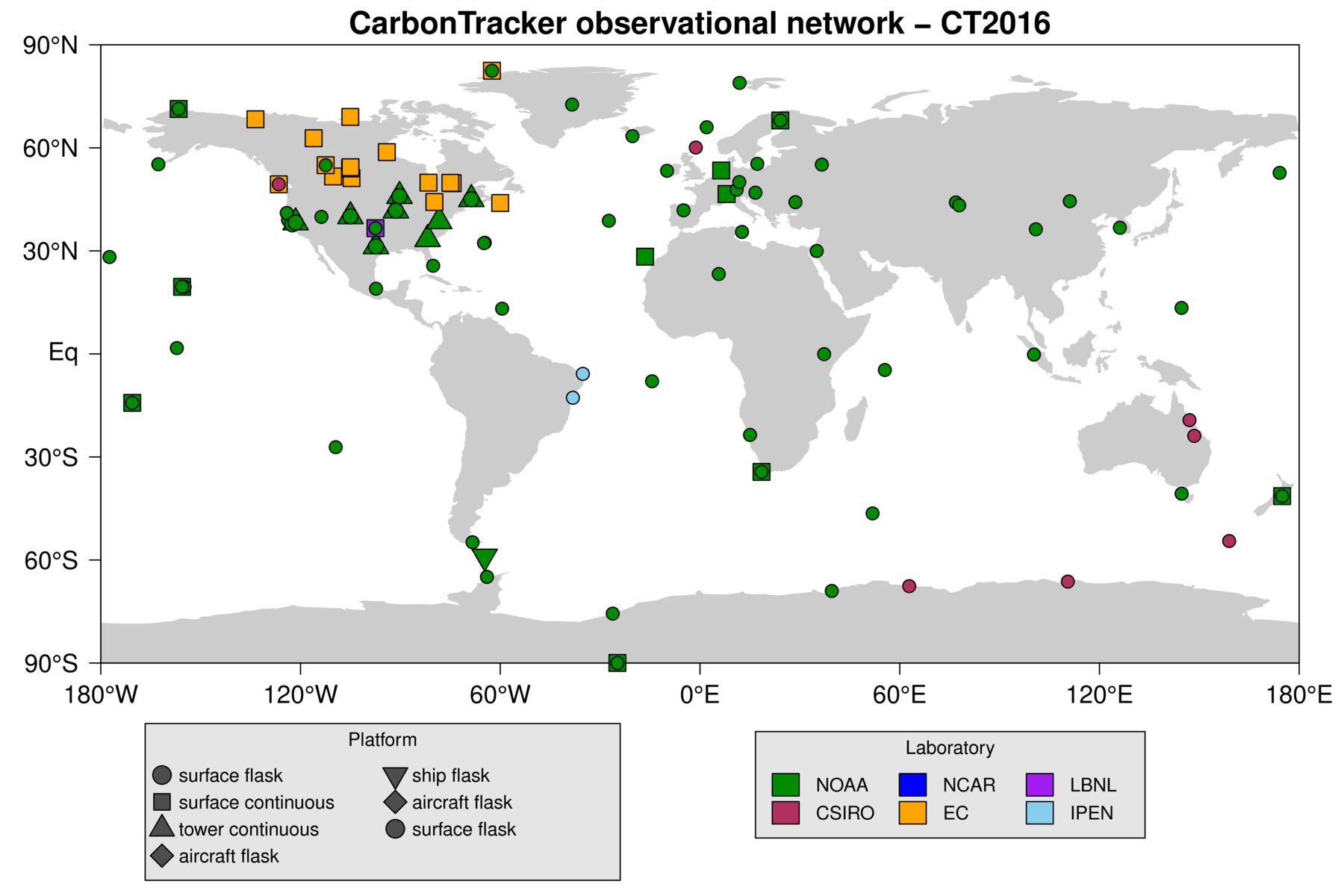
Figure 13: CarbonTracker global observational network. See
the CarbonTracker
interactive
network map for more details.
We apply a further selection criterion during the assimilation to
exclude non-marine boundary layer (MBL) observations that are very
poorly forecasted in our framework. We use the so-called model-data
mismatch in this process, which is the random error ascribed to each
observation to account for measurement errors as well as modeling errors
of that observation. We interpret an observed-minus-forecasted
mole fraction that exceeds 3 times the prescribed model-data mismatch as
an indicator that our modeling framework fails. This can happen for
instance when an air sample is representative of local exchange not
captured well by our 1° × 1° fluxes, when local meteorological
conditions are not captured by our offline transport fields, but also
when large-scale CO2 exchange is suddenly changed (e.g. fires, pests,
droughts) to an extent that can not be accommodated by our flux modules.
This last situation would imply an important change in the carbon cycle
and has to be recognized by the researchers when analyzing the results.
In accordance with the 3-sigma rejection criterion, about 0.2%
of the observations are discarded through this mechanism in our
assimilations.
7.2 Adaptive model-data mismatch
The statistical optimization method we use to constrain surface CO2 fluxes requires that each assimilation constraint is assigned a "model-data mismatch" (MDM) error value. This is meant to express the statistics of simulated-minus-observed CO2 observations we could expect if CarbonTracker were using perfect surface fluxes. Such deviations arise from many sources, including random noise in the measurement system, in situ variability that we do not expect to resolve in our model, and faults with the atmospheric transport model. Generally, transport and inverse model faults are the dominant terms in MDM values. The MDM is one of two major "tuning knobs" used to adjust the performance of our ensemble Kalman filter. The other is also an error quantity, meant to represent the expected error on our first-guess fluxes. Discussion of this prior covariance error can be found in section 8.2. Prior to CT2016, CarbonTracker used a single MDM value for each assimilation dataset. The NOAA continuous observations at the 396m level of the WLEF tower in northern Wisconsin, for example, were assigned a MDM of 3.0 ppm, meaning that the residuals between model-forecasted measurements and the actual observed concentrations are expected to be unbiased (i.e., have a mean of zero) and have a standard deviation of 3 ppm. In practice, however, we have found that it is far easier to simulate wintertime observations than those during summer. This is mainly due to higher ambient variability of CO2 in the summer. With CT2016, we have started to use a new empirical scheme to assign MDM values, using statistics of model performance from a preliminary inversion. The posterior residuals for each dataset are analyzed for equally-spaced intervals of one-tenth of a year. For each of these periods, bias and random error are combined to form total deviation from observed values. The assigned MDM is set to a constant fraction (currently 80%) of this total posterior error. This scaling is meant to force the assimilation scheme to extract as much information as possible from available observations. Our new scheme assigns observations from this dataset a variable MDM of between 1.6 ppm (in winter) and 7.9 ppm (in summer). The adaptive MDM scheme performs well in terms of average χ2, which in an optimally-tuned system should be close to 1.0 for each dataset (see Table 2). Notably, the seasonal variations of MDM successfully compensate for the higher ambient variability of CO2 at continental sites during the growing season. It is, however, an iterative process, requiring that we conduct a previous inversion. For various reasons, this previous inversion performed before CT2016 differs in significant aspects from the actual CT2016 inversions. These differences have led to MDM values which are slightly too large and thus average χ2 values which are generally smaller than the target of 1.0 (in some cases, as low as 0.2 or 0.3). The next iteration of CarbonTracker will be able to use the more recent CT2016 inversions to refine the adaptive MDM scheme. Duplicate observations are identified as those within 50 minutes temporally, 10m vertically, and 0.05 degrees of latitude and longitude laterally (nominally, about 5km). The MDM for such observations is inflated by √n, where n is the number of duplicates.7.3 Statistical performance of CT2016
Table 2 summarizes the datasets assimilated in CarbonTracker, and the performace of the assimilation scheme for each dataset. These diagnostics are useful for evaluating how well CarbonTracker does in simulating observed CO2.| Dataset | Lab. | Location | Latitude | Longitude | Elev. | Used | Rej. | R | χ2 | Bias | SE |
| (m) | (ppm) | (ppm) | (ppm) | ||||||||
| co2_abp_surface-flask_1_representative | NOAA | Arembepe, Bahia, Brazil | 12.77°S | 38.17°W | 1 | 101 | 0 | 0.6 - 2.5 | 0.21 | -0.38 | 0.64 |
| co2_abp_surface-flask_26_marine | IPEN | Arembepe, Bahia, Brazil | 12.77°S | 38.17°W | 1 | 103 | 1 | 0.8 - 4.6 | 0.35 | -0.67 | 1.28 |
| co2_alt_surface-flask_1_representative | NOAA | Alert, Nunavut, Canada | 82.45°N | 62.51°W | 190 | 873 | 0 | 0.4 - 2.8 | 0.53 | 0.06 | 0.54 |
| co2_alt_surface-flask_2_representative | CSIRO | Alert, Nunavut, Canada | 82.45°N | 62.51°W | 190 | 549 | 3 | 0.4 - 1.4 | 0.99 | 0.13 | 0.57 |
| co2_alt_surface-flask_4_representative | SIO | Alert, Nunavut, Canada | 82.45°N | 62.51°W | 190 | 363 | 1 | 0.4 - 2.9 | 0.63 | 0.23 | 0.54 |
| co2_alt_surface-insitu_6_allvalid | EC | Alert, Nunavut, Canada | 82.45°N | 62.51°W | 190 | 20010 | 131 | 0.4 - 2.7 | 0.76 | 0.05 | 0.60 |
| co2_amt_surface-pfp_1_allvalid | NOAA | Argyle, Maine, United States | 45.03°N | 68.68°W | 53 | 1015 | 3 | 1.5 - 10.9 | 0.33 | 0.28 | 3.15 |
| co2_amt_tower-insitu_1_allvalid-107magl | NOAA | Argyle, Maine, United States | 45.03°N | 68.68°W | 53 | 14188 | 63 | 2.2 - 14.6 | 0.34 | 0.36 | 3.24 |
| co2_ara_surface-flask_2_representative | CSIRO | Arcturus, Queensland, Australia | 23.86°S | 148.47°E | 175 | 20 | 0 | 2.9 - 7.1 | 0.43 | -0.37 | 3.00 |
| co2_asc_surface-flask_1_representative | NOAA | Ascension Island, United Kingdom | 7.97°S | 14.40°W | 85 | 1364 | 0 | 0.5 - 1.1 | 1.04 | 0.03 | 0.70 |
| co2_ask_surface-flask_1_representative | NOAA | Assekrem, Algeria | 23.26°N | 5.63°E | 2710 | 703 | 2 | 0.6 - 1.0 | 0.68 | -0.04 | 0.61 |
| co2_azr_surface-flask_1_representative | NOAA | Terceira Island, Azores, Portugal | 38.77°N | 27.38°W | 19 | 425 | 5 | 1.0 - 2.5 | 0.90 | 0.35 | 1.42 |
| co2_bal_surface-flask_1_representative | NOAA | Baltic Sea, Poland | 55.35°N | 17.22°E | 3 | 923 | 8 | 4.0 - 6.2 | 0.69 | -1.08 | 4.09 |
| co2_bao_surface-pfp_1_allvalid | NOAA | Boulder Atmospheric Observatory, Colorado, United States | 40.05°N | 105.00°W | 1584 | 2009 | 7 | 3.1 - 21.9 | 0.29 | -2.10 | 3.11 |
| co2_bao_tower-insitu_1_allvalid-300magl | NOAA | Boulder Atmospheric Observatory, Colorado, United States | 40.05°N | 105.00°W | 1584 | 9638 | 2 | 7.0 - 24.6 | 0.13 | -2.09 | 3.36 |
| co2_bck_surface-insitu_6_allvalid | EC | Behchoko, Northwest Territories, Canada | 62.80°N | 116.05°W | 179 | 3863 | 71 | 0.9 - 6.3 | 0.73 | -0.08 | 3.79 |
| co2_bhd_surface-flask_1_representative | NOAA | Baring Head Station, New Zealand | 41.41°S | 174.87°E | 85 | 187 | 1 | 0.6 - 1.3 | 0.75 | 0.06 | 0.55 |
| co2_bhd_surface-insitu_15_baseline | NIWA | Baring Head Station, New Zealand | 41.41°S | 174.87°E | 85 | 502 | 2 | 0.5 - 1.1 | 0.81 | 0.29 | 0.47 |
| co2_bkt_surface-flask_1_representative | NOAA | Bukit Kototabang, Indonesia | 0.20°S | 100.32°E | 845 | 355 | 3 | 3.7 - 5.1 | 0.82 | 2.10 | 3.60 |
| co2_bme_surface-flask_1_representative | NOAA | St. Davids Head, Bermuda, United Kingdom | 32.37°N | 64.65°W | 12 | 234 | 2 | 1.2 - 2.3 | 0.86 | 0.56 | 1.50 |
| co2_bmw_surface-flask_1_representative | NOAA | Tudor Hill, Bermuda, United Kingdom | 32.26°N | 64.88°W | 30 | 515 | 19 | 0.8 - 1.6 | 0.97 | 0.60 | 1.21 |
| co2_bra_surface-insitu_6_allvalid | EC | Bratt's Lake Saskatchewan, Canada | 51.20°N | 104.70°W | 595 | 6750 | 16 | 2.5 - 17.1 | 0.44 | -0.05 | 3.86 |
| co2_brw_surface-flask_1_representative | NOAA | Barrow, Alaska, United States | 71.32°N | 156.61°W | 11 | 810 | 13 | 0.6 - 3.6 | 1.03 | -0.01 | 1.00 |
| co2_brw_surface-insitu_1_allvalid | NOAA | Barrow, Alaska, United States | 71.32°N | 156.61°W | 11 | 12130 | 9 | 0.9 - 4.1 | 0.58 | 0.07 | 0.77 |
| co2_bsc_surface-flask_1_representative | NOAA | Black Sea, Constanta, Romania | 44.18°N | 28.66°E | 0 | 431 | 3 | 6.4 - 16.5 | 0.65 | -4.69 | 8.46 |
| co2_cba_surface-flask_1_representative | NOAA | Cold Bay, Alaska, United States | 55.21°N | 162.72°W | 21 | 1036 | 14 | 0.9 - 3.4 | 0.89 | -0.54 | 1.67 |
| co2_cba_surface-flask_4_representative | SIO | Cold Bay, Alaska, United States | 55.21°N | 162.72°W | 21 | 320 | 5 | 0.5 - 4.2 | 0.84 | -0.07 | 1.79 |
| co2_cby_surface-insitu_6_allvalid | EC | Cambridge Bay, Nunavut Territory, Canada | 69.01°N | 105.05°W | 35 | 3646 | 7 | 1.2 - 5.0 | 0.14 | 0.16 | 1.33 |
| co2_cdl_surface-insitu_6_allvalid | EC | Candle Lake, Saskatchewan, Canada | 53.99°N | 105.12°W | 600 | 11083 | 14 | 2.2 - 20.2 | 0.32 | 0.13 | 2.33 |
| co2_cfa_surface-flask_2_representative | CSIRO | Cape Ferguson, Queensland, Australia | 19.28°S | 147.06°E | 2 | 321 | 2 | 0.8 - 2.6 | 0.59 | -0.35 | 0.96 |
| co2_cgo_surface-flask_1_representative | NOAA | Cape Grim, Tasmania, Australia | 40.68°S | 144.69°E | 94 | 514 | 0 | 0.3 - 1.1 | 0.84 | 0.02 | 0.26 |
| co2_cgo_surface-flask_2_representative | CSIRO | Cape Grim, Tasmania, Australia | 40.68°S | 144.69°E | 94 | 783 | 6 | 0.3 - 1.3 | 0.75 | -0.00 | 0.29 |
| co2_cgo_surface-flask_4_representative | SIO | Cape Grim, Tasmania, Australia | 40.68°S | 144.69°E | 94 | 321 | 3 | 0.3 - 0.7 | 1.29 | 0.20 | 0.30 |
| co2_chl_surface-insitu_6_allvalid | EC | Churchill, Manitoba, Canada | 58.75°N | 94.07°W | 29 | 3891 | 53 | 0.8 - 3.6 | 0.78 | -0.09 | 1.68 |
| co2_chm_surface-insitu_6_allvalid | EC | Chibougamau, Quebec, Canada | 49.68°N | 74.30°W | 393 | 3728 | 13 | 2.9 - 12.1 | 0.29 | 0.00 | 2.57 |
| co2_chr_surface-flask_1_representative | NOAA | Christmas Island, Republic of Kiribati | 1.70°N | 157.15°W | 0 | 495 | 0 | 0.4 - 1.1 | 0.48 | -0.16 | 0.50 |
| co2_cib_surface-flask_1_representative | NOAA | Centro de Investigacion de la Baja Atmosfera (CIBA), Spain | 41.81°N | 4.93°W | 845 | 293 | 2 | 1.7 - 4.3 | 0.80 | 0.29 | 2.56 |
| co2_cps_surface-insitu_6_allvalid | EC | Chapais,Quebec, Canada | 49.82°N | 74.98°W | 381 | 5648 | 14 | 1.4 - 15.9 | 0.39 | 0.50 | 2.61 |
| co2_cpt_surface-flask_1_representative | NOAA | Cape Point, South Africa | 34.35°S | 18.49°E | 230 | 216 | 0 | 0.6 - 2.8 | 0.26 | -0.03 | 0.70 |
| co2_cpt_surface-insitu_36_marine | SAWS | Cape Point, South Africa | 34.35°S | 18.49°E | 230 | 106233 | 234 | 0.6 - 1.2 | 0.88 | 0.06 | 0.47 |
| co2_crz_surface-flask_1_representative | NOAA | Crozet Island, France | 46.43°S | 51.85°E | 197 | 599 | 0 | 0.3 - 0.4 | 0.81 | 0.02 | 0.26 |
| co2_cya_surface-flask_2_representative | CSIRO | Casey, Antarctica, Australia | 66.28°S | 110.52°E | 47 | 358 | 0 | 0.3 - 0.7 | 0.48 | -0.06 | 0.29 |
| co2_drp_shipboard-flask_1_representative | NOAA | Drake Passage, N/A | 59.00°S | 64.69°W | 0 | 189 | 1 | 0.3 - 0.7 | 0.42 | 0.04 | 0.28 |
| co2_egb_surface-insitu_6_allvalid | EC | Egbert, Ontario, Canada | 44.23°N | 79.78°W | 251 | 10418 | 51 | 4.2 - 19.7 | 0.25 | -0.83 | 4.37 |
| co2_eic_surface-flask_1_representative | NOAA | Easter Island, Chile | 27.16°S | 109.43°W | 47 | 467 | 5 | 0.8 - 1.2 | 1.10 | 0.45 | 1.03 |
| co2_esp_surface-flask_2_representative | CSIRO | Estevan Point, British Columbia, Canada | 49.38°N | 126.54°W | 7 | 23 | 0 | 0.3 - 5.0 | 0.97 | -0.59 | 1.14 |
| co2_esp_surface-insitu_6_allvalid | EC | Estevan Point, British Columbia, Canada | 49.38°N | 126.54°W | 7 | 6429 | 31 | 1.8 - 7.4 | 0.50 | -0.08 | 2.29 |
| co2_est_surface-insitu_6_allvalid | EC | Esther, Alberta, Canada | 51.66°N | 110.21°W | 707 | 5906 | 34 | 2.3 - 16.1 | 0.29 | -0.03 | 2.91 |
| co2_etl_surface-insitu_6_allvalid | EC | East Trout Lake, Saskatchewan, Canada | 54.35°N | 104.98°W | 492 | 13773 | 52 | 1.4 - 6.9 | 0.52 | 0.07 | 2.07 |
| co2_fsd_surface-insitu_6_allvalid | EC | Fraserdale, Canada | 49.88°N | 81.57°W | 210 | 20337 | 52 | 1.7 - 12.8 | 0.34 | 0.19 | 2.54 |
| co2_gmi_surface-flask_1_representative | NOAA | Mariana Islands, Guam | 13.39°N | 144.66°E | 0 | 917 | 16 | 0.7 - 1.1 | 0.79 | 0.08 | 0.77 |
| co2_hba_surface-flask_1_representative | NOAA | Halley Station, Antarctica, United Kingdom | 75.61°S | 26.21°W | 30 | 696 | 0 | 0.2 - 0.4 | 0.63 | 0.07 | 0.18 |
| co2_hpb_surface-flask_1_representative | NOAA | Hohenpeissenberg, Germany | 47.80°N | 11.02°E | 936 | 422 | 0 | 3.9 - 9.2 | 0.82 | 1.52 | 5.22 |
| co2_hun_surface-flask_1_representative | NOAA | Hegyhatsal, Hungary | 46.95°N | 16.65°E | 248 | 751 | 2 | 3.2 - 8.5 | 0.60 | -1.15 | 4.11 |
| co2_ice_surface-flask_1_representative | NOAA | Storhofdi, Vestmannaeyjar, Iceland | 63.40°N | 20.29°W | 118 | 408 | 1 | 1.0 - 1.6 | 0.38 | -0.06 | 0.77 |
| co2_inu_surface-insitu_6_allvalid | EC | Inuvik,Northwest Territories, Canada | 68.32°N | 133.53°W | 113 | 4105 | 26 | 0.8 - 5.7 | 1.04 | 0.25 | 1.94 |
| co2_izo_surface-insitu_27_allvalid | AEMET | Izana, Tenerife, Canary Islands, Spain | 28.31°N | 16.50°W | 2373 | 60761 | 224 | 0.9 - 1.4 | 0.56 | 0.13 | 0.74 |
| co2_jfj_surface-insitu_49_allvalid | KUP | Jungfraujoch, Switzerland | 46.55°N | 7.99°E | 3570 | 13233 | 129 | 1.8 - 4.4 | 0.51 | 0.06 | 1.99 |
| co2_jfj_surface-insitu_5_allvalid | EMPA | Jungfraujoch, Switzerland | 46.55°N | 7.99°E | 3570 | 7894 | 57 | 1.5 - 4.1 | 0.43 | 0.14 | 1.85 |
| co2_key_surface-flask_1_representative | NOAA | Key Biscayne, Florida, United States | 25.67°N | 80.16°W | 1 | 533 | 4 | 1.0 - 2.1 | 0.66 | 0.40 | 1.35 |
| co2_kum_surface-flask_1_representative | NOAA | Cape Kumukahi, Hawaii, United States | 19.52°N | 154.82°W | 3 | 955 | 9 | 0.8 - 2.6 | 0.60 | -0.14 | 0.99 |
| co2_kum_surface-flask_4_representative | SIO | Cape Kumukahi, Hawaii, United States | 19.52°N | 154.82°W | 3 | 524 | 12 | 0.8 - 2.7 | 0.54 | -0.14 | 1.31 |
| co2_kzd_surface-flask_1_representative | NOAA | Sary Taukum, Kazakhstan | 44.08°N | 76.87°E | 595 | 438 | 3 | 1.5 - 3.1 | 0.85 | -0.58 | 2.12 |
| co2_kzm_surface-flask_1_representative | NOAA | Plateau Assy, Kazakhstan | 43.25°N | 77.88°E | 2519 | 389 | 4 | 1.6 - 4.0 | 0.86 | 0.02 | 2.34 |
| co2_lef_surface-pfp_1_allvalid | NOAA | Park Falls, Wisconsin, United States | 45.95°N | 90.27°W | 472 | 1789 | 7 | 1.8 - 10.8 | 0.40 | -0.27 | 2.78 |
| co2_lef_tower-insitu_1_allvalid-396magl | NOAA | Park Falls, Wisconsin, United States | 45.95°N | 90.27°W | 472 | 20321 | 212 | 1.6 - 7.9 | 0.64 | -0.02 | 2.58 |
| co2_llb_surface-flask_1_representative | NOAA | Lac La Biche, Alberta, Canada | 54.95°N | 112.45°W | 540 | 154 | 3 | 2.3 - 11.3 | 0.52 | -0.64 | 3.67 |
| co2_llb_surface-insitu_6_allvalid | EC | Lac La Biche, Alberta, Canada | 54.95°N | 112.45°W | 540 | 10622 | 23 | 5.0 - 40.5 | 0.19 | 0.03 | 4.12 |
| co2_lmp_surface-flask_1_representative | NOAA | Lampedusa, Italy | 35.52°N | 12.62°E | 45 | 373 | 5 | 1.2 - 1.9 | 0.80 | 0.03 | 1.30 |
| co2_lut_surface-insitu_44_allvalid | RUG | Lutjewad, Netherlands | 53.40°N | 6.35°E | 1 | 9935 | 100 | 5.2 - 10.3 | 0.48 | -1.11 | 5.33 |
| co2_maa_surface-flask_2_representative | CSIRO | Mawson Station, Antarctica, Australia | 67.62°S | 62.87°E | 32 | 385 | 0 | 0.3 - 0.7 | 0.38 | -0.05 | 0.25 |
| co2_mex_surface-flask_1_representative | NOAA | High Altitude Global Climate Observation Center, Mexico | 18.98°N | 97.31°W | 4464 | 275 | 0 | 0.9 - 2.9 | 0.91 | 0.88 | 1.49 |
| co2_mhd_surface-flask_1_representative | NOAA | Mace Head, County Galway, Ireland | 53.33°N | 9.90°W | 5 | 630 | 4 | 0.8 - 1.6 | 0.59 | 0.03 | 0.95 |
| co2_mid_surface-flask_1_representative | NOAA | Sand Island, Midway, United States | 28.21°N | 177.38°W | 11 | 697 | 4 | 0.8 - 1.5 | 1.00 | 0.46 | 0.98 |
| co2_mkn_surface-flask_1_representative | NOAA | Mt. Kenya, Kenya | 0.06°S | 37.30°E | 3644 | 137 | 1 | 1.3 - 3.1 | 1.14 | 1.73 | 1.87 |
| co2_mlo_surface-flask_1_representative | NOAA | Mauna Loa, Hawaii, United States | 19.54°N | 155.58°W | 3397 | 1153 | 6 | 0.4 - 1.2 | 0.82 | 0.12 | 0.53 |
| co2_mlo_surface-flask_2_representative | CSIRO | Mauna Loa, Hawaii, United States | 19.54°N | 155.58°W | 3397 | 511 | 0 | 0.4 - 1.7 | 0.71 | 0.19 | 0.59 |
| co2_mlo_surface-flask_4_representative | SIO | Mauna Loa, Hawaii, United States | 19.54°N | 155.58°W | 3397 | 575 | 10 | 0.5 - 1.3 | 0.85 | 0.02 | 3.89 |
| co2_mlo_surface-insitu_1_allvalid | NOAA | Mauna Loa, Hawaii, United States | 19.54°N | 155.58°W | 3397 | 15671 | 0 | 0.6 - 1.2 | 0.50 | 0.17 | 0.45 |
| co2_mqa_surface-flask_2_representative | CSIRO | Macquarie Island, Australia | 54.48°S | 158.97°E | 6 | 449 | 0 | 0.3 - 0.7 | 0.56 | -0.01 | 0.30 |
| co2_nat_surface-flask_1_representative | NOAA | Farol De Mae Luiza Lighthouse, Brazil | 5.80°S | 35.19°W | 50 | 190 | 0 | 0.9 - 2.2 | 0.55 | -0.56 | 0.91 |
| co2_nat_surface-flask_26_marine | IPEN | Farol De Mae Luiza Lighthouse, Brazil | 5.80°S | 35.19°W | 50 | 200 | 1 | 0.6 - 2.2 | 0.77 | -0.52 | 1.01 |
| co2_nmb_surface-flask_1_representative | NOAA | Gobabeb, Namibia | 23.58°S | 15.03°E | 456 | 321 | 0 | 0.5 - 1.4 | 0.65 | -0.09 | 0.84 |
| co2_obn_surface-flask_1_representative | NOAA | Obninsk, Russia | 55.11°N | 36.60°E | 183 | 133 | 0 | 3.9 - 10.2 | 0.50 | 0.16 | 4.40 |
| co2_oxk_surface-flask_1_representative | NOAA | Ochsenkopf, Germany | 50.03°N | 11.81°E | 1009 | 355 | 4 | 2.9 - 4.9 | 0.83 | -0.54 | 3.67 |
| co2_pal_surface-flask_1_representative | NOAA | Pallas-Sammaltunturi, GAW Station, Finland | 67.97°N | 24.12°E | 560 | 580 | 6 | 1.4 - 6.7 | 0.66 | -0.34 | 2.22 |
| co2_pal_surface-insitu_30_marine | FMI | Pallas-Sammaltunturi, GAW Station, Finland | 67.97°N | 24.12°E | 560 | 23306 | 35 | 0.8 - 3.1 | 0.59 | 0.03 | 0.78 |
| co2_poc_shipboard-flask_1_representative | NOAA | Pacific Ocean, N/A | 0 | 2234 | 32 | 0.6 - 2.6 | 0.48 | -0.00 | 0.74 | ||
| co2_psa_surface-flask_1_representative | NOAA | Palmer Station, Antarctica, United States | 64.92°S | 64.00°W | 10 | 762 | 0 | 0.3 - 0.8 | 0.39 | -0.03 | 0.22 |
| co2_psa_surface-flask_4_representative | SIO | Palmer Station, Antarctica, United States | 64.92°S | 64.00°W | 10 | 354 | 4 | 0.2 - 0.6 | 0.79 | 0.14 | 0.22 |
| co2_pta_surface-flask_1_representative | NOAA | Point Arena, California, United States | 38.95°N | 123.74°W | 17 | 391 | 5 | 3.2 - 6.7 | 0.71 | -1.03 | 4.00 |
| co2_rpb_surface-flask_1_representative | NOAA | Ragged Point, Barbados | 13.16°N | 59.43°W | 15 | 736 | 4 | 0.8 - 1.1 | 0.57 | 0.08 | 0.64 |
| co2_sct_tower-insitu_1_allvalid-305magl | NOAA | Beech Island, South Carolina, United States | 33.41°N | 81.83°W | 115 | 9742 | 48 | 3.8 - 7.3 | 0.53 | -0.85 | 3.66 |
| co2_sey_surface-flask_1_representative | NOAA | Mahe Island, Seychelles | 4.68°S | 55.53°E | 2 | 684 | 0 | 0.5 - 1.3 | 1.03 | -0.03 | 0.76 |
| co2_sgp_surface-flask_1_representative | NOAA | Southern Great Plains, Oklahoma, United States | 36.61°N | 97.49°W | 314 | 610 | 9 | 2.0 - 9.3 | 0.82 | -0.98 | 3.33 |
| co2_sgp_surface-insitu_64_allvalid-60magl | LBNL-ARM | Southern Great Plains, Oklahoma, United States | 36.61°N | 97.49°W | 314 | 10104 | 18 | 3.4 - 17.4 | 0.28 | -0.46 | 3.29 |
| co2_shm_surface-flask_1_representative | NOAA | Shemya Island, Alaska, United States | 52.71°N | 174.13°E | 23 | 360 | 5 | 0.8 - 3.7 | 0.90 | -0.30 | 1.99 |
| co2_sis_surface-flask_2_representative | CSIRO | Shetland Islands, Scotland | 60.09°N | 1.25°W | 30 | 89 | 0 | 0.6 - 2.1 | 0.68 | 0.56 | 0.94 |
| co2_smo_surface-flask_1_representative | NOAA | Tutuila, American Samoa | 14.25°S | 170.56°W | 42 | 1156 | 2 | 0.3 - 2.1 | 0.58 | -0.08 | 0.48 |
| co2_smo_surface-flask_4_representative | SIO | Tutuila, American Samoa | 14.25°S | 170.56°W | 42 | 344 | 1 | 0.4 - 4.3 | 0.57 | 0.01 | 0.68 |
| co2_smo_surface-insitu_1_allvalid | NOAA | Tutuila, American Samoa | 14.25°S | 170.56°W | 42 | 16432 | 0 | 0.4 - 4.2 | 0.23 | -0.02 | 0.41 |
| co2_snp_tower-insitu_1_allvalid-17magl | NOAA | Shenandoah National Park, United States | 38.62°N | 78.35°W | 1008 | 8562 | 153 | 2.5 - 6.5 | 0.91 | 0.58 | 4.95 |
| co2_spo_surface-flask_1_representative | NOAA | South Pole, Antarctica, United States | 89.98°S | 24.80°W | 2810 | 803 | 0 | 0.2 - 1.3 | 0.52 | 0.10 | 0.19 |
| co2_spo_surface-flask_4_representative | SIO | South Pole, Antarctica, United States | 89.98°S | 24.80°W | 2810 | 367 | 0 | 0.2 - 1.2 | 0.69 | 0.13 | 0.20 |
| co2_spo_surface-insitu_1_allvalid | NOAA | South Pole, Antarctica, United States | 89.98°S | 24.80°W | 2810 | 21457 | 2 | 0.2 - 1.4 | 0.47 | 0.02 | 0.15 |
| co2_stm_surface-flask_1_representative | NOAA | Ocean Station M, Norway | 66.00°N | 2.00°E | 0 | 840 | 9 | 0.7 - 2.0 | 0.63 | 0.11 | 0.94 |
| co2_str_surface-pfp_1_allvalid | NOAA | Sutro Tower, San Francisco, California, United States | 37.76°N | 122.45°W | 254 | 1551 | 37 | 1.9 - 4.0 | 0.70 | -0.53 | 2.61 |
| co2_sum_surface-flask_1_representative | NOAA | Summit, Greenland | 72.60°N | 38.42°W | 3210 | 665 | 10 | 0.5 - 1.0 | 0.85 | 0.11 | 0.71 |
| co2_syo_surface-flask_1_representative | NOAA | Syowa Station, Antarctica, Japan | 69.01°S | 39.59°E | 14 | 369 | 0 | 0.2 - 0.4 | 0.39 | -0.03 | 0.19 |
| co2_tap_surface-flask_1_representative | NOAA | Tae-ahn Peninsula, Republic of Korea | 36.74°N | 126.13°E | 16 | 635 | 8 | 2.6 - 6.6 | 0.69 | -0.30 | 3.07 |
| co2_thd_surface-flask_1_representative | NOAA | Trinidad Head, California, United States | 41.05°N | 124.15°W | 107 | 559 | 19 | 2.1 - 5.8 | 0.79 | -1.49 | 3.46 |
| co2_ush_surface-flask_1_representative | NOAA | Ushuaia, Argentina | 54.85°S | 68.31°W | 12 | 396 | 0 | 0.6 - 1.0 | 0.71 | -0.39 | 0.51 |
| co2_uta_surface-flask_1_representative | NOAA | Wendover, Utah, United States | 39.90°N | 113.72°W | 1327 | 644 | 5 | 1.1 - 2.5 | 0.82 | 0.32 | 1.73 |
| co2_uum_surface-flask_1_representative | NOAA | Ulaan Uul, Mongolia | 44.45°N | 111.10°E | 1007 | 713 | 10 | 1.9 - 3.6 | 0.86 | -0.23 | 2.77 |
| co2_wbi_surface-pfp_1_allvalid | NOAA | West Branch, Iowa, United States | 41.72°N | 91.35°W | 242 | 1901 | 9 | 2.8 - 19.8 | 0.40 | -0.74 | 4.07 |
| co2_wbi_tower-insitu_1_allvalid-379magl | NOAA | West Branch, Iowa, United States | 41.72°N | 91.35°W | 242 | 10586 | 64 | 3.0 - 12.8 | 0.56 | -0.43 | 3.73 |
| co2_wgc_surface-pfp_1_allvalid | NOAA | Walnut Grove, California, United States | 38.27°N | 121.49°W | 0 | 1521 | 6 | 6.4 - 27.0 | 0.41 | -2.56 | 7.16 |
| co2_wgc_tower-insitu_1_allvalid-483magl | NOAA | Walnut Grove, California, United States | 38.27°N | 121.49°W | 0 | 10200 | 104 | 4.6 - 8.6 | 0.51 | -0.05 | 4.41 |
| co2_wis_surface-flask_1_representative | NOAA | Weizmann Institute of Science, Kibbutz Ketura, Israel | 29.96°N | 35.06°E | 151 | 775 | 7 | 1.4 - 3.4 | 0.82 | -0.44 | 2.03 |
| co2_wkt_surface-pfp_1_allvalid | NOAA | Moody, Texas, United States | 31.31°N | 97.33°W | 251 | 1914 | 12 | 2.2 - 11.6 | 0.39 | -0.65 | 2.52 |
| co2_wkt_tower-insitu_1_allvalid-457magl | NOAA | Moody, Texas, United States | 31.31°N | 97.33°W | 251 | 15879 | 194 | 2.7 - 8.2 | 0.58 | -0.38 | 2.59 |
| co2_wlg_surface-flask_1_representative | NOAA | Mt. Waliguan, Peoples Republic of China | 36.29°N | 100.90°E | 3810 | 559 | 17 | 1.1 - 2.0 | 0.85 | 0.07 | 1.48 |
| co2_wsa_surface-insitu_6_allvalid | EC | Sable Island, Nova Scotia, Canada | 43.93°N | 60.02°W | 5 | 14581 | 244 | 1.6 - 3.5 | 0.63 | -0.10 | 2.16 |
| co2_zep_surface-flask_1_representative | NOAA | Ny-Alesund, Svalbard, Norway and Sweden | 78.91°N | 11.89°E | 474 | 800 | 6 | 0.7 - 1.4 | 0.77 | 0.13 | 0.82 |
7.4 References
- ESRL Carbon Cycle Program
- WMO/GAW Report No. 168, 2006
- Thoning, K. W., P. P. Tans, and W. D. Komhyr (1989), Atmospheric carbon dioxide at Mauna Loa Observatory: 2. Analysis of the NOAA GMCC data, 1974–1985, J. Geophys. Res., 94(D6), 8549–8565, doi:10.1029/JD094iD06p08549.
8 Ensemble data assimilation
Data assimilation is the process by which a model simulation is adjusted to agree with observations. Model simulations may drift off from reality for a number of reasons. Some models are highly nonlinear, and depend sensitively on knowing the system state with high accuracy. Weather models fall into this category, and as a result reliable forecast systems depend on having a constant stream of meteorological data to correct their simulations. In contrast, models like CarbonTracker need data assimilation not because the controlling dynamics are nonlinear, but because those dynamics are not well known. CarbonTracker uses approximate or estimated rules about the evolution of surface CO2 fluxes, then corrects these approximate projections using observational constraints. The resulting optimal surface flux estimates can then be used to better understand the functioning of the carbon cycle. Data assimilation is usually a cyclical process, in which estimates get refined over time as more observations become available. Mathematically, data assimilation can be performed using a wide variety of techniques, including variational and ensemble methods. Assimilation systems involving simulations of the global atmosphere are often implemented on highly parallel supercomputers in order to distribute the workload among many computational cores. CarbonTracker is an exmaple of such a model because it relies heavily on estimates of global atmospheric transport. CarbonTracker model predictions are mainly limited by the relatively simple representations of CO2 surface exchange used to predict land biosphere and ocean fluxes and emissions from fossil fuel combustion and wildfires. As described in the following section, we use data assimilation techniques to modify these surface fluxes so that the resulting atmospheric distribution of CO2 agrees optimally with measurements. We do this by estimating a set of spatially- and temporally-varying scaling factors that multiply first-guess predictions from prior flux models. Data assimilation allows us to determine optimal values for these scaling factors.8.1 Parameterization of unknowns
CO2 fluxes F(x,y,t) in CarbonTracker are parameterized according to
| (11) |
8.1.1 Optimization regions
The scaling factors λ are estimated independently for each week and optimization region. They are assumed to be constant over this time period and spatial domain. Each scaling factor is associated with a particular region of the globe, as in the TransCom inversion study (e.g. Gurney et al., 2002). Currently the geographic distribution of these optimization regions is fixed. The choice of regions is a strong a priori design decision determining the reliability of the resulting fluxes. In particular, the scale of optimization regions is chosen to minimize "aggregation errors" (Kaminski et al., 2001), while limiting the set of unknown parameters to a manageable number. Following Jacobson et al. (2007), we have divide the global ocean into 30 basins encompassing large-scale ocean circulation and biogeochemical features. The terrestrial biosphere is divided up according to ecosystem type and geographical domain. Specifically, each of the 11 TransCom land regions is subdivided into a maximum of 19 "ecoregions" according to its Olson (1992) vegetation classification. The set of ecoregions over North America is summarized in Table 3 and Figure 17. Note that there is currently no requirement for ecoregions to be contiguous, and a single scaling factor can be applied to the same vegetation type on both sides of a continent. Further details on ecoregions can be found in Section 9 Theoretically, this approach leads to a total number of 11*19+30=239 optimizable scaling factors for each week, but the actual number of optimization regions is only 156 since some ecosystem types are not represented in every TransCom region. It should be noted also that we have chosen to not optimize scaling factors for ice-covered regions, inland water bodies, and deserts, since the CO2 flux from these regions is negligible. It is important to note that even though only one parameter is available to scale, for instance, the flux from coniferous forests in Boreal North America, each 1° × 1° grid box predominantly covered by coniferous forests will have a different optimized flux λFland(x,y,t) depending on local temperature, radiation, and emissions as simulated by the prior flux model. Ecosystem types are based on the vegetation classification of Olson, (1992). Note that we have adjusted the original 29 categories into only 19 regions. This was done mainly to fill the unused categories 16, 17, and 18, and to group the similar categories 23-26+29. Table 3 shows each vegetation category considered. Percentages indicate the relative area in North America associated with each category.| category | Olson V 1.3 | Percentage area |
| 1 | Conifer Forest | 19.0% |
| 2 | Broadleaf Forest | 1.3% |
| 3 | Mixed Forest | 7.5% |
| 4 | Grass/Shrub | 12.6% |
| 5 | Tropical Forest | 0.3% |
| 6 | Scrub/Woods | 2.1% |
| 7 | Semitundra | 19.4% |
| 8 | Fields/Woods/Savanna | 4.9% |
| 9 | Northern Taiga | 8.1% |
| 10 | Forest/Field | 6.3% |
| 11 | Wetland | 1.7% |
| 12 | Deserts | 0.1% |
| 13 | Shrub/Tree/Suc | 0.1% |
| 14 | Crops | 9.7% |
| 15 | Conifer Snowy/Coastal | 0.4% |
| 16 | Wooded tundra | 1.7% |
| 17 | Mangrove | 0.0% |
| 18 | Non-optimized areas (ice, polar desert, inland seas) | 0.0% |
| 19 | Water | 4.9% |
Table 2: Ecosystem types over North America
Each 1° × 1° pixel of our domain was assigned one of the categories
above based on the Olson category that was most prevalent in the 0.5°×0.5° underlying area.
8.1.2 Ensemble size and localization
The ensemble system used to solve for the scalar multiplication factors is similar to that in Peters et al. (2005) and based on the square root ensemble Kalman filter of Whitaker and Hamill (2002). We have restricted the length of the smoother window to only five weeks as we found the derived flux patterns within North America to be robustly resolved well within that time. We caution users of CarbonTracker results that although North American flux estimates have been determined to be robust after five weeks, regions of the world with less dense observational coverage (the tropics, Southern Hemisphere, and parts of Asia) are likely to be poorly observable even after more than a month of transport and therefore less robustly resolved. Although longer assimilation windows, or long prior covariance length-scales, could potentially help to constrain larger scale emission totals from such areas, we focus our analysis here on a region more directly constrained by atmospheric observations. Ensemble statistics are created from 150 ensemble members, each with its own background CO2 concentration field to represent the time history (and thus covariances) of the filter. Approximation of the covariance matrix by a discrete ensemble can result in apparent improvements in modeled measurements from fluxes that are unphyiscally remote. To dampen such spurious correlations, we apply localization (Houtekamer and Mitchell, 1998) for certain datasets. Localization is not used for datasets judged to represent hemisphere-scale signals, such as those from marine boundary layer sites in remote locations. Localization ensures that datasets of continental observations within North America do not determine, for example, tropical African fluxes, unless a very robust signal is found. In contrast, marine boundary layer datasets with a known large footprint and strong capacity to see integrated flux signals are not localized. Localization is based on the linear correlation coefficient between the 150 parameter deviations and 150 observation deviations for each parameter. If the relationship between a parameter deviation and its modeled observational impact is statistically significant, then that relationship is used to modify parameters. Otherwise, the relationship is assumed to be spurious noise due to the numerical approximation of the covariance matrix by the limited ensemble. We accept relationships that reach 95% significance in a Student's T-test with a two-tailed probability distribution.8.1.3 Dynamical model
In CarbonTracker, the dynamical model is applied to the ensemble-mean parameter values λ as:
| (12) |
8.2 Covariance structure
The prior covariance structure P−0 describes the magnitude of the uncertainty on each parameter, plus their correlation in space. The latter is applied such that correlations between the same ecosystem types in different TransCom regions decrease exponentially with distance (L=2000km), and thus assumes a coupling between the behavior of the same ecosystems in close proximity to one another (such as coniferous forests in Boreal and Temperate North America). Furthermore, all ecosystems within tropical TransCom regions are coupled decreasing exponentially with distance since we do not believe the current observing network can constrain tropical fluxes on sub-continental scales, and want to prevent spurious compensating source/sink pairs ("dipoles") to occur in the tropics. In our standard assimilation, the chosen standard deviation is 80% on land parameters. All parameters have the same variance within the land or ocean domain. Because the parameters multiply the net-flux though, ecosystems with larger weekly mean net fluxes have a larger variance in absolute flux magnitude.8.3 Multiple prior models
In Bayesian estimation systems like CarbonTracker, there is a potential for bias from a flux prior to propagate through the inversion system to the final result. It is difficult to quantify this effect, and as a result it is generally considered a requirement that flux priors be unbiased. We cannot guarantee this for any of our prior fluxes, be they the prior estimates for terrestrial or oceanic exchange, or the presumed wildfire and fossil fuel emissions. In order to explicitly quantify the impact of prior bias on our solution, in CT2016 we present the result of a multi-model prior suite of inversions. We have used two terrestrial flux priors (including two wildfire emissions estimates), two air-sea CO2 exchange priors, and two estimates of imposed fossil fuel emissions in a factorial design experiment. For each of the resulting eight unique combinations of prior fluxes, we conduct an independent inversion conducted independently according to the methods described above. We present as a final result the mean flux across this suite of inversions and the atmospheric CO2 distribution resulting from applying these mean fluxes to our atmospheric transport model. Each of the priors is described in detail in its corresponding documentation section.
Figure 14: CT2016 prior covariance structure. The prior
covariance matrix (top panel) and the square root of diagonal members of
this matrix (bottom panel). Covariance matrix quantities are
dimensionless squared scaling factors, and the bottom panel is the
square root of this. TransCom land
regions form the first 11 large divisions on the axes here. As
described above, each of those regions contains 19 potential ecosystems.
Correlations between similar ecosystems in proximate TransCom regions
are visible in North America (e.g. NABR and NATM, the boreal and
temperate North American regions) and Eurasia. Within tropical TransCom
regions, however, differing ecosystems are assigned a non-zero prior
covariance, which is visible here as red block-like structures on the
diagonal within, for example, the South America Tropical (SATR) TransCom
region. Ocean regions have a more complicated covariance structure that
depends on which prior is used; the structure shown here is that of the
ocean inversion flux prior. The
lower panel of this diagram compares the on-diagonal elements of the
prior covariance matrix by plotting their square roots. The resulting
standard deviations are directly comparable to the percentages discussed
in section 3 above; 0.8 is equivalent to 80%. The retuning of the
covariance matrix for CT2016's multiple-prior simulation is made
evident by also showing these values from previous CarbonTracker
releases in light blue.
8.3.1 Posterior uncertainties in CarbonTracker
The formal "internal" error estimates produced by CarbonTracker are unrealistically large. This is largely a result of the relatively short assimilation window in CarbonTracker, along with a dynamical model that introduces a fresh prior covariance matrix with every new week entering the assimilation window. This five-week window effectively inhibits the formation of anticorrelations ("dipoles") in flux estimates, and does little to reduce the confidence interval on prior fluxes. The temporal truncation in CarbonTracker imposed by its five-week assimilation window tends to yield regional flux estimates that are largely uncorrelated with those from other regions. A consequence of this feature is that uncertainties in CarbonTracker tend to increase as larger regions are considered; regional errors mostly just add in quadrature without any cancellation from dipole anticorrelation. Whereas many inversions yield smaller errors as the spatial extent of the region being considered increases, CarbonTracker acts in the opposite fashion. This is perhaps most obvious in the estimate of CarbonTracker's global annual surface flux of carbon dioxide. While CT2016 estimates a one-sigma error of more than 6 PgC yr−1 on its global flux, this quantity is in actuality much more well-constrained. This is evident from CarbonTracker's excellent agreement with observational estimates of atmospheric growth rate. In CT2016, error estimates are about a factor of two larger than in previous releases, mainly due to the retuning of the land prior covariance discussed above. However, uncertainties presented for CT2016 take into account not only the "internal" flux uncertainty generated by a single inversion, but also the across-model "external" uncertainty representing the spread of the inversion models due to the choice of prior flux.8.4 References
- Jeffrey S. Whitaker and Thomas M. Hamill, 2002: Ensemble Data
Assimilation without Perturbed Observations. Mon. Wea. Rev.,
130, 1913–1924.
doi: http://dx.doi.org/10.1175/1520-0493(2002)130<1913:EDAWPO>2.0.CO;2 - Peters, W., M. C. Krol, E. J. Dlugokencky, F. J. Dentener, P. Bergamaschi, G. Dutton, P. v. Velthoven, J. B. Miller, L. Bruhwiler, and P. P. Tans (2004), Toward regional-scale modeling using the two-way nested global model TM5: Characterization of transport using SF6, J. Geophys. Res., 109, D19314, doi:10.1029/2004JD005020
- Olson ecosystem types
- Kaminski, T., P. J. Rayner, M. Heimann, and I. G. Enting (2001), On aggregation errors in atmospheric transport inversions, J. Geophys. Res., 106(D5), 4703–4715, doi:10.1029/2000JD900581.
9 Ecoregions in CarbonTracker
9.1 What are ecoregions?
Ecoregions are the actual scale on which CarbonTracker performs its optimization over land. Ecoregions are meant to represent large expanses of land within a given continent having similar ecosystem types, and are used to divide continent-scale regions into smaller domains for analysis. The ecosystem types use in CarbonTracker are derived from the Olson (1992) vegetation classification (Table 4, Figure 15). We define an ecoregion as an ecosystem type within a given TransCom land region. There are 11 such TransCom land regions (Figure 16), so there are 11*19 = 209 possible ecoregions. However, not all ecosystem types are present in all TransCom regions, and the actual number of land ecoregions ends up being 126. Note on "Semitundra": this is a potentially misleading shorthand abbreviation for a collection of ecosystems comprising semi-desert, shrubs, steppe, and polar+alpine tundra. The "Semitundra" zones appearing in northern Africa where one expects to find the Sahara desert are not, of course, tundra environments. They are instead semi-desert zones.
Figure 15: Global distribution of Olson ecosystem types.
| Ecosystem Type | North American Boreal | North American Temperate | ||
| Area (km2) | Percentage | Area (km2) | Percentage | |
| Conifer Forest | 2315376 | 22.9% | 1607291 | 14.0% |
| Broadleaf Forest | - | - | 269838 | 2.4% |
| Mixed Forest | 592291 | 5.9% | 930813 | 8.1% |
| Grass/Shrub | 53082 | 0.5% | 2515582 | 21.9% |
| Tropical Forest | - | - | 58401 | 0.5% |
| Scrub/Woods | - | - | 416520 | 3.6% |
| Semitundra | 3396292 | 33.6% | 866468 | 7.6% |
| Fields/Woods/Savanna | 29243 | 0.3% | 1020939 | 8.9% |
| Northern Taiga | 1658773 | 16.4% | - | - |
| Forest/Field | 61882 | 0.6% | 1243174 | 10.8% |
| Wetland | 322485 | 3.2% | 66968 | 0.6% |
| Deserts | - | - | 21934 | 0.2% |
| Shrub/Tree/Suc | - | - | 11339 | 0.1% |
| Crops | - | - | 1969912 | 17.2% |
| Conifer Snowy/Coastal | 41440 | 0.4% | 73437 | 0.6% |
| Wooded tundra | 360388 | 3.6% | 6643 | 0.1% |
| Mangrove | - | - | - | - |
| Non-optimized areas | - | - | - | - |
| Water | 1269485 | 12.6% | 384728 | 3.4% |
| Total | 10100736 | 100.0% | 11463986 | 100.0% |
Table 3: Ecosystem areas over the two TransCom regions covering North America.
9.2 Why use ecoregions?
A fundamental challenge to atmospheric inversions like CarbonTracker is that there are not enough observations to directly constrain fluxes at all times and in all places. It is therefore necessary to find a way to reduce the number of unknowns being estimated. Strategies to reduce the number of unknowns in problems like this one generally impose information from external sources. In CarbonTracker, we reduce the problem size both by estimating fluxes at the ecoregion scale, and by using a terrestrial biological model to give a first guess flux from the ecoregion. The model is also used to give the spatial and temporal distribution of CO2 flux within a region and week.9.3 Ecosystems within TransCom regions
Each TransCom land region (Figure 16) can contain up to 19 ecoregions.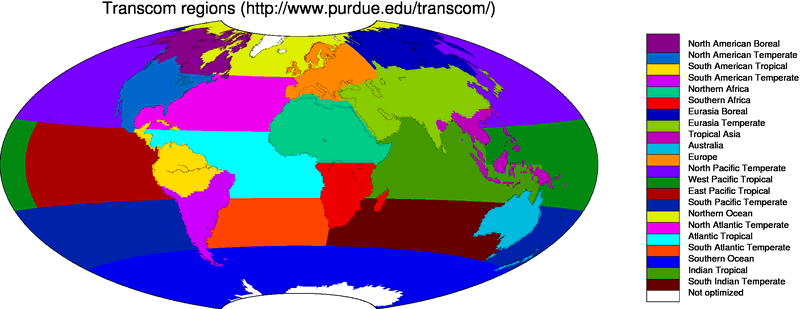
Figure 16: The 11 land regions and 11 ocean regions of the TransCom project
.
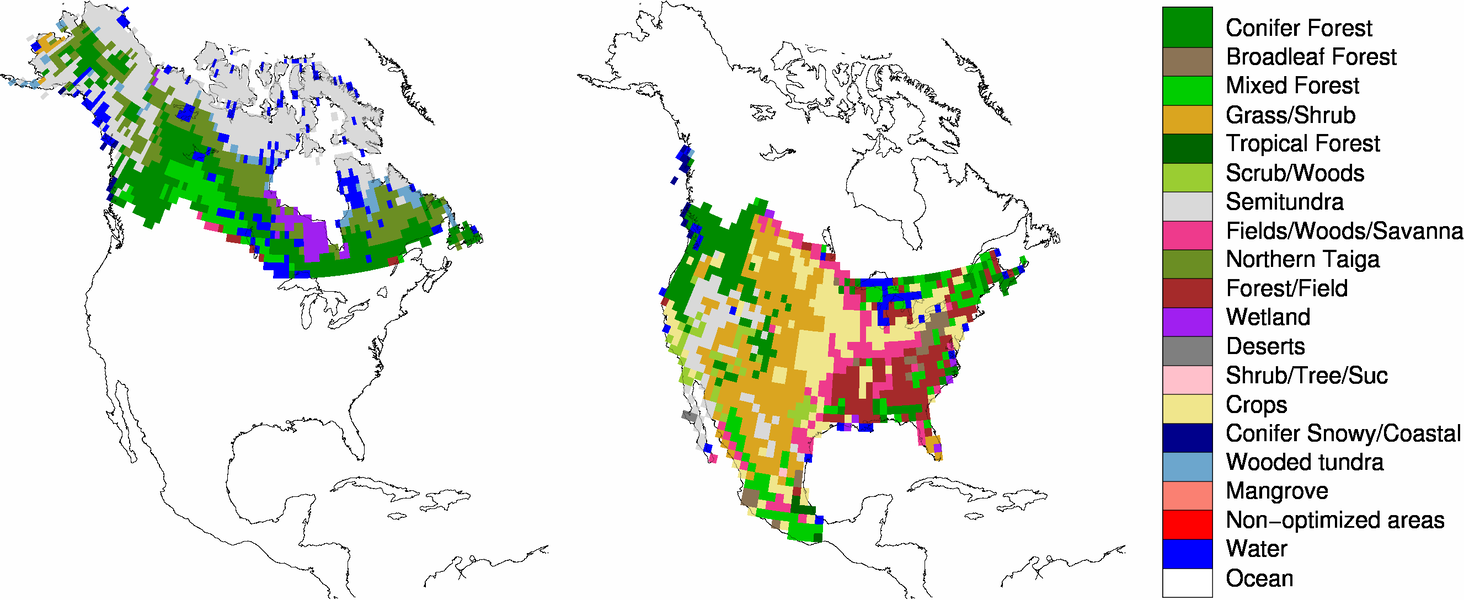
Figure 17: Ecoregions within the North American Boreal (left)
and North American Temperate (right) TransCom regions.
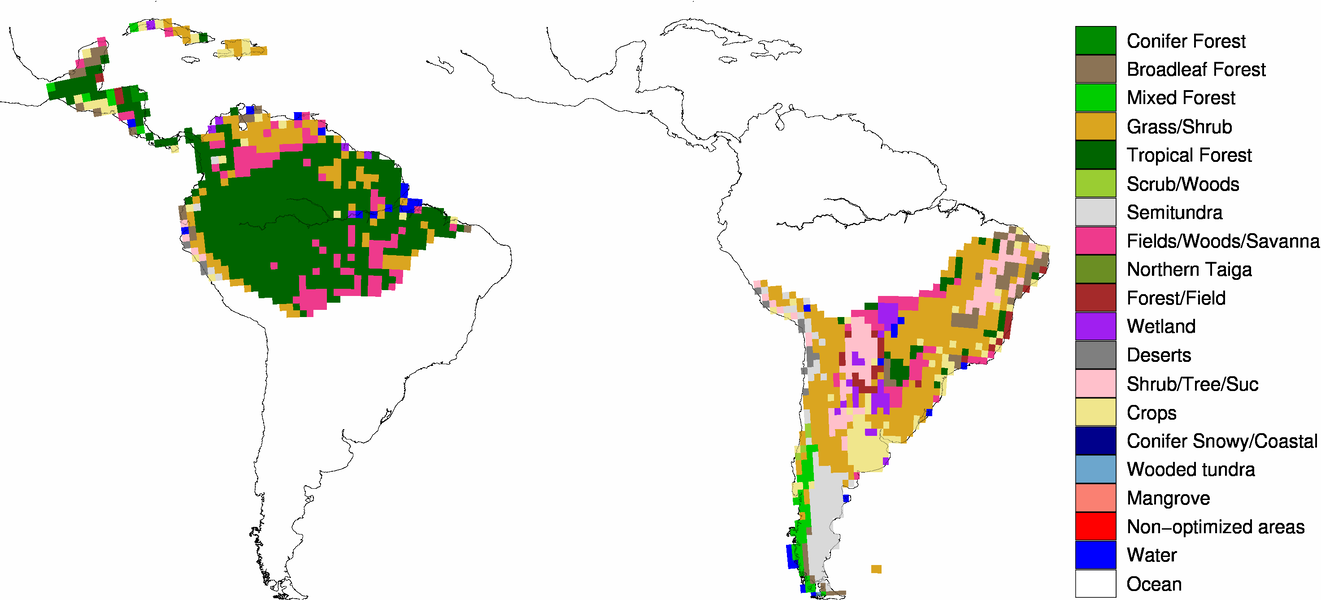
Figure 18: Ecoregions within the South American Tropical (left)
and South American Temperate (right) TransCom regions.
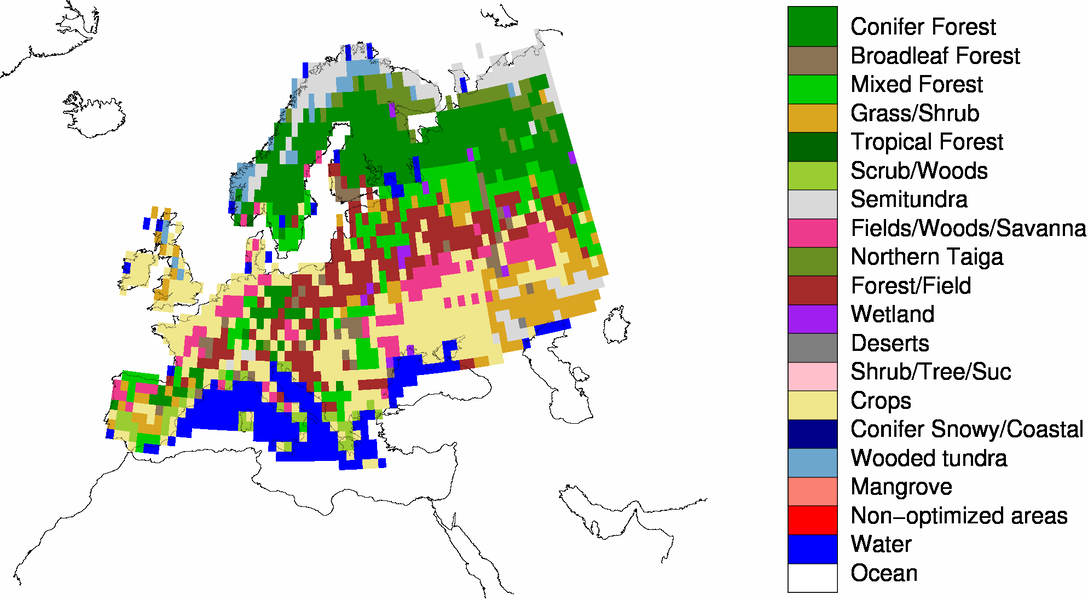
Figure 19: Ecoregions within the Europe TransCom region.
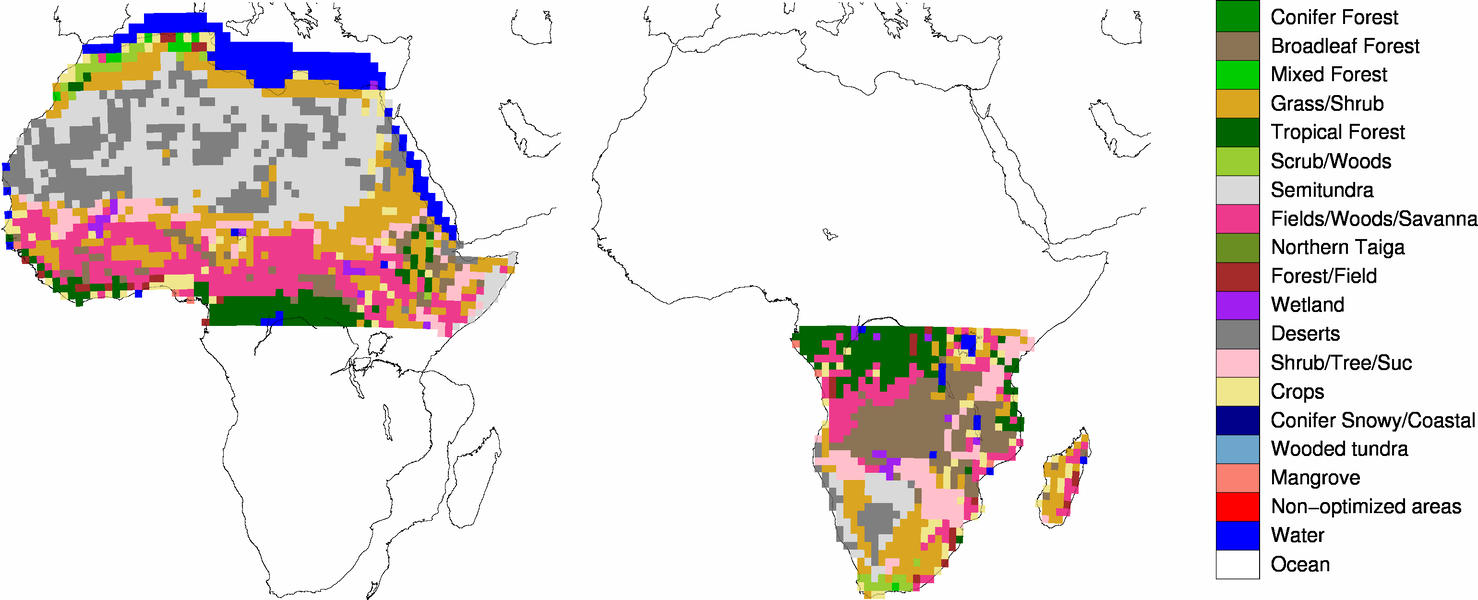
Figure 20: Ecoregions within the Northern Africa (left) and
Southern Africa (right) TransCom regions.
9.4 References
File translated from TEX by TTH, version 4.04.
On 17 Feb 2017, 13:45.

