Ozone Measurement Principle and Theory
2.1 Total Ozone Observations
Total ozone observations are made with the Dobson spectrophotometer by measuring the relative intensities of selected pairs of ultraviolet wavelengths, called the A, B*, C, C', and D wavelength pairs, emanating from the sun, moon or zenith sky. The A wavelength pair, for example, consists of the 3055 A.U. wavelength that is highly absorbed by ozone, and the more intense 3254 A.U. wavelength that is relatively unaffected by ozone. Outside the earth's atmosphere the relative intensity of these two wavelengths remains essentially fixed. In passing through the atmosphere to the instrument, however, both wavelengths lose intensity because of scattering of the light by air molecules and dust particles; additionally, the 3055 A.U. wavelength is strongly attenuated while passing through the ozone layer whereas the attenuation of the 3254 A.U. wavelength is relatively weak. The relative intensity of the A wavelengths as seen by the instrument, therefore, varies with the amount of ozone present in the atmosphere since as the ozone amount increases the observed intensity of the 3055 A.U. wavelength decreases, whereas the intensity of the 3254 A.U. wavelength remains practically unaltered. Thus, by measuring the relative intensities of suitably selected pair wavelengths with the Dobson instrument, it is pcssible to determine how much ozone is present in a vertical column of air extending from ground level to the top of the atmosphere in the neighborhood of the instrument. The result is expressed in terms of a thickness of a layer of pure ozone at standard temperature and pressure.
*[Observations on B wavelengths are not needed for determinations of total ozone, but they are useful for research into the accuracy of ozone measurements.]
Detailed information concerning derivation of the mathematical equations used in reducing total ozone measurement data obtained from observations on direct sun or moon are given elsewhere (Dobson, 1957a). A summary of the relevant equations is given below.
For ozone observations made on single pair wavelengths such as the A, B, C, or D pair, the general data reduction equation is
X = {N - (beta-beta')mp/p0 - (delta-delta')sec Z}/(alpha-&alpha')mu ,
where
X = total amount of ozone expressed in Dobson units (1 DU = 10-5 m pure ozone at STP), or in atmo-cm;
N = L0 - L = log (I0/I'0) - log (I/I') ;
I0 and I0' = intensities outside the atmosphere of solar radiation at the short and long wavelengths, respectively, of the wavelength pair;
I and I' = measured intensities at the ground of solar radiation at the short and long wavelengths, respectively;
beta and beta' = Rayleigh scattering coefficients of air at the short and long wavelengths, respectively;
m = ratio of the actual and vertical paths of solar radiation through the atmosphere, taking into account refraction and the earth's curvature;
p = observed station pressure;
p0 = mean sea level pressure;
delta and delta' = scattering coefficients of aerosol particles at the short and long wavelengths, respectively;
Z = angular zenith distance of the sun;
alpha and alpha' = absorption coefficients of ozone at the short and long wavelengths, respectively;
mu = ratio of the actual and vertical paths of solar radiation through the ozone layer, the mean height of the ozone layer being 22 km.
A difficulty arises in using equation (1) since no satisfactory method is available for estimating the value of the aerosol scattering coefficient (delta-delta'). In practice, therefore, observations are normally made on double pair wavelengths, e.g., the AD wavelengths. Since both the A and the D wavelength pairs are approximately equally scattered by the atmosphere, the scattering effect is nearly canceled so that absorption by ozone becomes by far the major factor affecting the relative intensities of the double pair wavelengths on which observations are made.
For ozone observations made on double pair wavelengths such as the AD, BD, CD, or AC pair, the general data reduction equation is
N1 - N2 - [(beta-beta')1 - (beta-beta')2]mp/p0 - [(delta-delta')1 - (delta-delta')2]sec Z
X12 = ------------------------------------------------------------------------------------------
[(alpha-alpha')1 - (alpha-alpha')2]mu
where the subscripts 1, 2 refer to the two wavelength pairs and (delta-delta')1 - (delta-delta')2 is assumed to equal zero. Here, also, mean station pressure may be used for p without significant error.
Total ozone amounts can also be deduced from observations on the clear or cloudy zenith sky. The zenith sky data are reduced by means of empirically constructed charts which relate instrument N, mu, and X values. Such charts are drawn using quasi-simultaneously obtained data from direct sun observations and observations on the clear or cloudy zenith. Detailed information concerning methods and data reduction are presented in Sections 6.2.4 and 7.3 of this manual.
2.2 0zone Vertical Distribution (Umkehr) Observations
If Dobson spectrophotometer observations are made on the clear zenith sky during a one-half day, and observed instrument N values are plotted vs. time, a maximum in the N values is observed to occur shortly after sunrise or before sunset. This reversal (or "Umkehr") in the plotted curve is related to the effective scattering height in the atmosphere of the wavelengths on which observations are made. Coupled with information on standard ozone profiles and a knowledge of the total ozone amount, the Umkehr data can be analyzed to yield ozone vertical distributions that reveal changes in ozone associated with day-to-day weather conditions as well as with seasonal and long-term trends.
The method of Umkehr data analysis was originally developed by Götz, Meetham and Dobson (1934). In recent years, the method has been refined by Ramanathan and Dave (1957) and Mateer and Dütsch (1964). At present, observational Umkehr data are routinely submitted to the World Ozone Data Center (WODC), Canadian Atmospheric Environment Service, Downsview, Ontario, for processing according to standardized techniques.
2.3 Principle of Operation of the Spectrophotometer
The principle of operation of the ozone spectrophotometer is best explained with reference to Figure 1. Light enters the instrument through a window in the top of the instrument and, after reflection in a right-angled prism, falls on slit S1 of a spectroscope. This spectroscope consists of a quartz lens which renders the light parallel, a prism which breaks up the lights into its spectral colors, and a mirror which reflects the light back through the prism and lens to form a spectrum in the focal plane of the instrument. The required wavelengths are isolated by means of slits S2, S3, and S4 located at the instrument's focal plane.
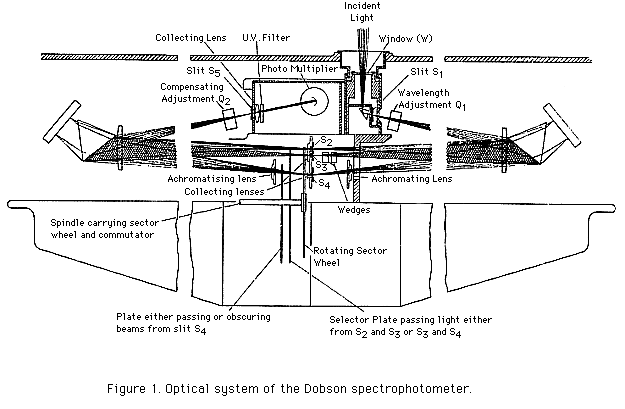
Two shutter rods are mounted in the base of the spectrophotometer. The left-hand S4 shutter rod is used only when spectrophotometer tests are conducted, and should be pushed all the way into the instrument when ozone observations are made. The right-hand wavelength selector rod blocks out light passing either through slit S2 or S4. When this rod is set to position SHORT, only slits S2 and S3 are open so that observations can be made on A, B, C, or D wavelength pairs. With the wavelength selector rod in the LONG position, only slits S3 and S4 are open and observations can be made on the C' wavelengths.
Selection of the wavelengths A, B, C, C', or D when making ozone measurements is accomplished by rotating Q1 and Q2 levers to positions specified in a Table of Settings of Q provided with the instrument. Thick, flat quartz plates mounted immediately in front of the first and last slits (S1 and S5) are fixed to the Q levers. Depending on the direction in which the quartz plates are rotated, the light beam passing through them is refracted upwards or downwards, thereby providing for wavelength selection. Changes in the refractive index of the spectrophotometer quartz prisms due to changes in the temperature of the instrument are allowed for by making slight adjustments to the settings of Q1.
An optical wedge, consisting of two quartz flats coated with chromel, is mounted in the instrument in front of slit S3. The position of the wedge is controlled by turning a graduated dial located on top of the instrument. With the dial set at 0° the thin portion of the optical wedge is positioned in front of slit S3 so that light passes through the optical wedge and slit S3 with practically no loss of intensity. With the dial set at 300°, however, the S3 light beam is almost completely absorbed by the thick portion of the optical wedge. It follows that there exists a "balance" setting of the dial somewhere between 0° and 300° where the intensity of the light beam passing through the optical wedge and slit S3 will have been reduced to the level of the intensity of the S2 wavelength beam (or S4 wavelength beam if observations on C' wavelengths are made). Now, for any given position of the dial the intensity of the light passing through the optical wedge is reduced in a definite ratio which is determined during the original calibration of the spectrophotometer. In order to measure the relative intensity of the two wavelengths on which observations are made, then, it is necessary only to be able to detect the balance position of the dial.
Indication of the balance position of the dial is effected in the following manner. Assume that the dial is initially set off-balance so that the two light beams leaving slit S3 and slit S2 (or slit S4) are of unequal intensity. The light beams then pass through a rotating sector wheel, driven by a motor, which chops them and allows them to proceed alternately into a second monochronometer and, finally, to fall on the photomultiplier located behind slit S5. (The purpose of the second monochronometer is to eliminate scattered light.) Since the two light beams falling alternately on the photomultiplier are of unequal intensity, they give rise to a pulsating electron current flowing out of the photomultiplier. This current is amplified by an alternating current amplifier, rectified by a commutator, and causes a deflection on an indicating direct current microammeter. If now the dial is turned to the balance position, the two light beams falling alternately on the photomultiplier become of equal intensity. They then give rise to a steady, direct current which cannot be amplified by an alternating current amplifier. Since there is no pulsating current to amplify and rectify, the microammeter reads zero. Thus, a null reading on the microammeter is an indication of the balance position of the dial. The relative intensities of the two wavelengths on which observations are made may then be obtained from the balance position dial reading and calibration tables supplied with the instrument.
Return to Table of Contents
Forward to Section 3. Calibration of a Dobson Spectrophotometer