APPENDIX H
INTRODUCTION TO PRINCIPLES OF ASTRONOMY
1. Celestial Sphere
The celestial sphere is an imaginary globe of infinite radius at whose center is located the earth. In the "shell" of the sphere are embedded the stars and the sun. The earth is imagined to be fixed, and the celestial sphere to be rotating from east to west, its axis being the prolongation of that of the earth. Thus, to the naked eye the pole star remains nearly stationary.
The portion of the celestial sphere seen by the observer is the hemisphere above the plane of his own horizon. A vertical line at the position of the observer coincides with the plumb line and is normal to the observer's horizon plane. The point in intersection of the vertical line and celestial sphere boundary is the zenith. A corresponding point in the opposite hemisphere is called the observer's nadir.
The celestial equator is the great circle formed by the intersection of the earth's equatorial plane with the surface of the celestial sphere.
The celestial poles are the points where the extended earth's axis pierces the celestial sphere.
2. Observer's Position on Earth
The position of any point on the surface of a sphere may be fixed by angular measurement from two planes of reference at right angles to each other passing through the centre of the sphere; these measurements are called the spherical coordinates of that point. The spherical coordinates of any station on the earth are designated as the latitude and longitude of the station.
The latitude of a station is defined as the angular distance of the station below or above the equator. When the station is above the equator, the latitude is north and its sign is positive, e.g., +47° or 47°. When below the equator, the latitude of the station is south and its sign is negative.
A parallel is the line joining all points which are at the same latitude, i.e., parallel to the equatorial circle.
A meridian circle is any circle on the surface of the earth passing through both the north and south poles.
The longitude of a station is defined as the angular distance measured along the arc of the equator between a primary meridian, which is a reference meridian, and the meridian circle passing through the station. The primary meridian most generally used is that of Greenwich, England. Longitudes are expressed either in degrees or arc or in hours of time (15° = 1 hr.) and are measured either east or west of the Greenwich meridian.
3. Position of a Celestial Body
Two systems of coordinates are commonly used to describe the position of a celestial body. If it is required only to specify a star's position on the celestial sphere, the right ascension system of coordinates is employed. When the position of a star with respect to the meridian through a given station on the surface of the earth is to be determined, the hour angle system of coordinates is used.
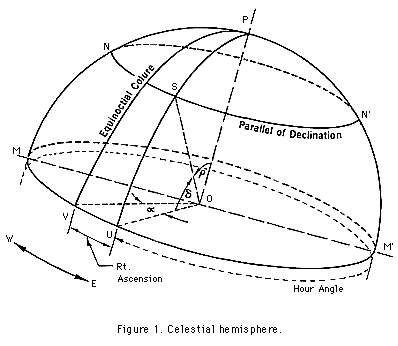
(a) Right Ascension Coordinate System. In Figure 1, S is a celestial body on the celestial hemisphere whose position is to be fixed by spherical coordinates. The earth is located at the centre, O, of the sphere with its axis in the direction of OP.
Hour circles on the celestial sphere compare with the meridian circles or meridians of longitude of the earth. In the figure, PSU is an hour circle arc.
Parallels of declination of the celestial sphere compare with the parallels of latitude of the earth.
The equinoctial colure of the celestial sphere passes through the vernal equinox, V, an imaginary point among the stars where the sun apparently crosses the equator from south to north on March 21 of each year. The E.C. compares with the prime meridian through Greenwich.
Right ascension of the sun or any star (comparable to the longitude of a station on earth) is the angular distance, alpha, measured along the celestial equator between the vernal equinox and the hour circle through the body. Right ascensions are measured eastward from the vernal equinox and may be expressed in degrees of arc (0° to 360°) or in hours of time (0h to 24h).
Declination of any celestial body is the angular distance, delta, of the body above or below the celestial equator. It is comparable with the latitude of the station on earth. If the body is above the equator its declination is said to be north and is considered as positive; if it is below the equator its declination is said to be south and is considered negative. Declinations are expressed in degrees and cannot exceed 90° in magnitude.
Polar distance of any celestial body is = 90° - delta with due regard to the sign of the declination.
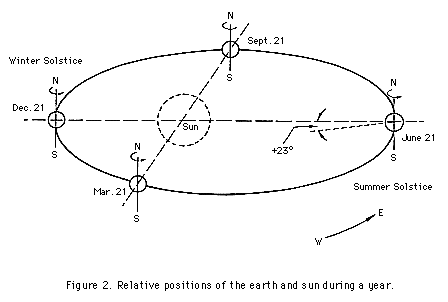
For the present purpose the vernal equinox is assumed to be a fixed point on the celestial equator. However, the coordinates of celestial bodies with respect to the celestial equator and the equinoctial colure change slightly with the passage of time. The fixed stars, or those outside the solar system, alter their positions in the celestial sphere only slightly from month to month and from year to year, the annual change being less than a minute of arc in either right ascension or declination. These variations result from precession or the slow change in the direction of the earth's axis caused by attraction of the sun, moon and planets, and nutation or small inequalities in the motion of precession. Proper motion of stars also occurs, that is, stars actually move very slightly with respect to the celestial sphere as time goes on. Furthermore, aberration, or an apparent change in position of heavenly bodies occurs, with a period of one year, because of the combined effect of the motion of light and motion of the observer fixed on the moving earth. Finally, the angle subtended by lines drawn from any star to the earth and sun changes continuously as the earth makes its annual circuit around the sun. As a result, the positions of the stars seem to change on the celestial sphere due to parallax.
As the earth actually travels around the sun but not the stars, (see Figure 2) the sun appears to move more slowly than the stars, making in 1 year 365 apparent revolutions (approx.) while the stars make 366 apparent revolutions (approx.); thus, the sun apparently makes a complete circuit of the heavens once each year, a new cycle beginning every March 21. Furthermore, as the axis of rotation of the earth is not normal to the plane of the earth's orbit, the path apparently traced by the sun among the stars on the celestial sphere, called the ecliptic, is a continuous curved line; each year the sun crosses the equator northward on March 21, and reaches a maximum positive declination (about 23.5° N) on June 21.
(b) The Hour Angle Coordinate System. In Figure 1, let the plane of the hour circle MNPN'M' coincide at the time of observation with the plane of the observer's meridian circle, and let S be some heavenly body whose position with respect to the observer's meridian and the equator MM'UV it is desired to establish. The spherical coordinates of the star are given by (1) the angular distance of the star above or below the equator, which in the figure is given by the arc US, defined previously as the declination, and (2) the angular distance measured along the equator between the meridian and the hour circle through the star. When this measurement is from east to west it is called an hour angle. The hour angle of any celestial body may then be defined as the angular distance measured westward along the equator from the meridian of reference to the hour circle through the body. Hour angles are expressed either in hours of time or in degrees of arc. In the figure, the hour angle is more than 12h or more than 180°. When no qualification is stated, it is understood that an hour angle is measured from the upper branch of the meridian, that is, the branch above the station or above the observer's head. Sometimes the hour angles of stars east of the observer's meridian are reckoned from the upper branch of the meridian rather than westward. An hour angle expressed in this way is preceded by a minus sign.
4. Equator Systems Compared
The system of coordinates described in article (b) is seen to be similar, to that described in article (a) with this difference, that in the hour angle system, the angular distance along the equator is measured (westward) from a fixed meridian, whereas in the right ascension system the angular distance along the equator is measured (eastward) from the vernal equinox, which is a point on the celestial equator that rotates with the celestial sphere. Thus, although right ascensions of fixed stars have annual variations of but a few seconds, hour angles of the stars change as rapidly as the celestial sphere apparently rotates (24h or 360° for each 36h 56h of our civil time), and hour angles of the sun change approximately 24h or 360° for each 24h of our civil time.
The two systems are called equatorial systems of coordinates, since in each case the primary plane of reference is the celestial equator. The declination, delta, is the same in both systems.
5. The Astronomical Triangle
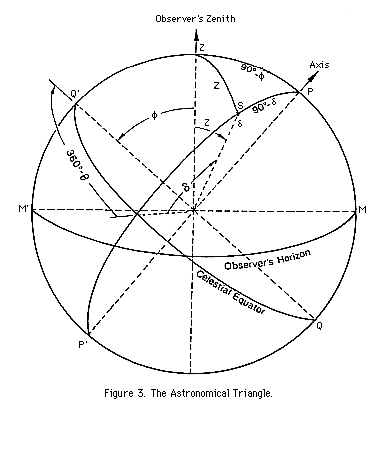
In Figure 3, the celestial sphere is pictured once again. The earth is imagined to be located at the center of the sphere with its polar axis in the direction P'P.
The observer's meridian plane lies in the plane of the great circle MQ'ZPMQP' and the star S is in a position east of the the meridian and above the celestial equator. The place of observation is assumed to be north of the equator at a latitude phi as shown by the angle between the equatorial plane and the observer's zenith plumb line. The hour angle, theta, is measured from the upper branch of the meridian (360° - theta is shown in the figure). The declination, delta, is also shown.
The colatitude (90° - phi), the zenith distance (Z), and the polar distance (90° - delta) define a spherical triangle the vertices of which are the pole P, the zenith Z, and the celestial body S. This triangle is called the astronomical triangle.
The determination of the relationship between theta and Z, 90° - phi and 90° - delta of the astronomical triangle is a problem in spherical trigonometry which is dealt with in many elementary mathematical texts. It is sufficient to quote the result here:
This is the equation that must be solved for cos Z to obtain mu.
Return to Table of Contents
Forward to Appendix I. Concept of Time